2.3. Einige Beispiele

Betrachten wir dazu einige Beispiele, die deutlich machen, wie das Regalmodell die Energiespeicherung darstellt. Zunächst soll die Grundregel erläutert werden. In der folgenden Abbildung sehen Sie drei Regale.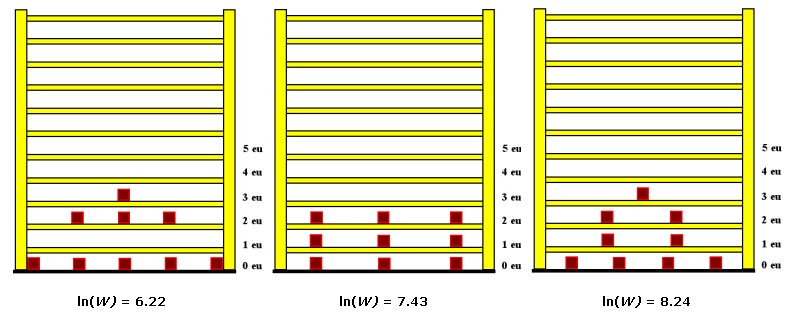

Drei Regale

In allen drei Fällen:     9 Teilchen mit 9 Energieeinheiten  (hier abgekürzt eu 'energy unit')

Zur Beschreibung natürlicher Phänomene ist eigentlich nur das rechte Regal ist von Bedeutung, da hier die Energie auf möglichst viele, nämlich 4, Fachböden verteilt ist. Zudem sind es auch die untersten 4 Niveaus und die Besetzungszahlen nehmen nach oben hin ab. Dies entspricht der Grundregel und es erscheint auch plausibel. Die Natur beginnt die Speicherung auf den unteren Niveaus, erst wenn es dort "eng" wird, kommen höhere "Fachböden" dran. Es werden keine Energiepakete auf unnötig hohen Niveaus eingelagert. Diese Verteilung nennt man Boltzmann-Verteilung. Ungünstig sind Anordnungen, bei denen ein hoch liegendes Niveau stärker besetzt ist als ein darunter liegendes Niveau, wie im linken Regal.

Alle drei Verteilungen zeigen Makrozustände (s. dazu Erläuterungen zur Grundregel), bei denen Gesamtenergie und Teilchenzahl gleich sind, die sich jedoch in der Verteilung der Energie auf die vorgegebenen Niveaus (entspricht einer vorgegebenen Stoffart) unterschieden. Im linken Regal ist ein Makrozustand dargestellt, zu dem es 503 Mikrozustände (ln(503)=6,22) gibt, im mittleren sind es bereits 1686 Mikrozustände (ln(1686)=7,43) und im rechten Regal handelt es sich um die dominante Verteilung mit 3790 Mikrozuständen (ln(3790)=8,42). Es ist der dominante Makrozustand für diese 9 Teilchen in diesem Energie-Eigenwertsystem und der vorgegebenen Gesamtenergie von 9 Energieeinheiten eu.

Die Entropie berechnet man nach folgenden Beziehungen:
Konvention

Für die Entropie wird häufig die Beziehung S = R . ln(W) angegeben, die auf Ludwig Boltzmann zurückgeht. Da Änderungen der Entropie verständlicherweise nicht von der Konstanten R sondern nur von dem Term ln(W) herkommen können und es häufig auf die Entropieänderungen ankommt, ist es zweckmäßig nur diesen Teil der Beziehung als fundamentale Entropie σ zu bezeichnen, so wie es KITTEL und KRÖMER vorgeschlagen haben.
Einer der Vorteile dieser Festlegung besteht darin, dass sich die Einheit der Entropie ändert und dadurch von einem "Energieeinfluss" befreit wird. Die Einheit der konventionellen Entropie S, die J/(K.mol) beträgt, war vermutlich die Hauptursache aller Missdeutungen des Entropiephänomens, weil mit dieser Einheitenkombination der Zusammenhang der Entropie mit der Anzahl der Mikrozustände nicht erkennbar wird. Die Entropie σ = S/R hingegen erscheint auf den ersten Blick als reine Zahl, die nur eine Quantitätsangabe, aber keine Qualitätsaussage macht.
Der Quotient S/R ist aber (s. o.) gleich dem Logarithmus des statistischen Gewichts W der dominanten energetischen Teilchenverteilung über die gequantelten Energieniveaus ist und er beschreibt die abzählbare Menge der Mikrozustände. Die Qualität der Abzählbarkeit dieser Zustände geht diesem Phänomen jedoch nicht verloren, nur weil man diese Anzahl logarithmiert.

Ein weiterer Vorteil ergibt sich durch den Zusammenhang zwischen Entropie und Temperatur. Auch das Temperaturphänomen wird durch die Festlegung von KITTEL und KRÖMER mit der fundamentalen Temperatur τ = RT wesentlich klarer beschrieben. In den folgenden Abschnitten wird dies näher erläutert.

Grundregal b Grundregal 10N Werden die Teilchen eines Systems / Stoffes von niedrigeren auf höhere Niveaus umge- lagert, so ändert sich dadurch die Temperatur des Systems. Die Anzahl der besetzten Niveaus und damit die Entropie nehmen zu.
Links:
niedrige Temperatur,
8 besetzte Niveaus,
geringere Entropie
Rechts:
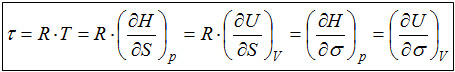
höhere Temperatur,
10 besetzte Niveaus,
höhere Entropie.


1. Die Definitionsgleichungen für die Temperatur T (bzw. der fundamentalen Temperatur τ = RT) in der (klassischen) Thermodynamik:
Temperatur 1

(H: Enthalpie ; U: innere Energie ;
S: konventionelle Entropie ; σ: fundamentale Entropie ;
p: Druck ; V: Volumen)


2. Die Definitionsgleichung für die Temperatur T (bzw. der fundamentalen Temperatur τ = RT) auf der Grundlage der Energiequantelung:
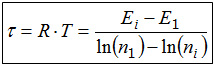
Temperatur 2

(k: Boltzmann-Konstante ; Ei : Energie des i-ten Niveaus ; ni : Besetzungszahl des i-ten Niveaus)

Ein Vergleich der beiden Temperaturdefinitionen zeigt, dass es sich in beiden Fällen um Quotienten handelt. Da in beiden Fällen im Zähler eine Energiedifferenz steht, kann man schließen, dass auch die Nenner in beiden Fällen eine gleichartige Qualität haben müssen. An der zweiten Temperaturdefinition ersieht man leicht, dass es sich um die Qualität einer Anzahl handelt, denn die Besetzungszahlen der Energieniveaus sind natürliche Zahlen, schließlich kann man keine halben Teilchen im "Regal" einlagern. Durch das Logarithmieren geht der Anzahlcharakter nicht verloren. Wird die Temperatur durch kT oder besser RT* beschrieben, so würde man dies auch an der Einheit kJ/mol erkennen können.

Die Anzahlen, auf die die Energie bezogen wird, sind die Anzahlen der Mikrozustände, die das System oder der Stoff mit der entsprechenden Energie annehmen könnte. Die Anzahl der Mikrozustände ist für Substanzen unter alltäglichen Bedingungen so groß, dass sie jedes menschliche Vorstellungsvermögen für Zahlen übersteigt. Für 100g Kochsalz oder 10 Liter Helium ergeben sich Werte in der Größenordnung von 103.1024Stück.

Die Anzahl der Mikrozustände nimmt jedoch mit der Anzahl der besetzten Energieniveaus monoton zu. Deshalb ist es zulässig, vereinfachend zu sagen: Die Entropie ist ein Maß für die Anzahl der besetzten Energieniveaus. Und diese Vereinfachung ist auch sinnvoll, denn die Anzahl der besetzten Niveaus liegt in einer anschaulich leicht fassbaren Größenordnung. Für 10 Liter Helium liegt sie im Bereich von ca. 2000 besetzten Niveaus.

Eine mathematische Besonderheit der Exponentialfunktion läßt sich nutzen, um die thermodynamische Definition der Temperatur auf der Basis der Energiequantelung zu vereinfachen. Diese Besonderheit liegt darin, dass nach stets gleichen Änderungen der unabhängigen Variablen (hier die Energie) sich die Funktionswerte halbieren. Diese Eigenschaft ist vielen vom radioaktiven Zerfall her vertraut. Dort dient sie dazu, die Schnelligkeit des Zerfalls zu charakterisieren: Man gibt die Halbwertzeit an, denn die unabhängige Variable ist beim radioaktiven Zerfall die Zeit. In völliger Analogie dazu kann man hier von der Halbwertsenergie EH sprechen, also von der zusätzlichen Energiehöhe, nach der sich die Besetzungszahl ni eines Niveaus im Vergleich zu einem Ausgansgniveau n1 halbiert:

EH = Ei - E1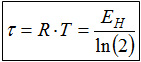
ni /n1 = 0,5   ⇒   ln(n1) - ln(ni) = ln(2).

Halbwertsenergie

* (Der Unterschied zwischen der Boltzmann-Konstanten k und der Gaskonstanten R besteht nur aus einem Einheitenwechsel. Korrekterweise sollte bei einer Einheitenumrechnung auf beiden Seiten des Gleichheitszeichens ein Zahlenwert und ein Einheitensymbol stehen: 1 mol = 6,02214 . 1023 stück.
Man erhält dann k = 1,38066 . 10-23 JK-1stück-1 = 8,31453 JK-1mol-1 = R.
Für das Verständnis der thermodynamischen Zusammenhänge erscheint nicht es als hilfreich, beim Wechsel einer Einheit auch das Symbol für die Größenart zu ändern, schließlich sind Größenwerte unabhängig von den jeweils verwendeten Einheiten.)