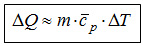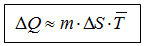Die Grundversion

Bei Flaschen/Gefäßen mit konstantem Querschnitt bestimmt stets die Querschnittsfläche A das Fassungsvermögen solcher Flaschen/Gefäße bis zu einer bestimmten Füllhöhe. Übertragen bedeutet dies: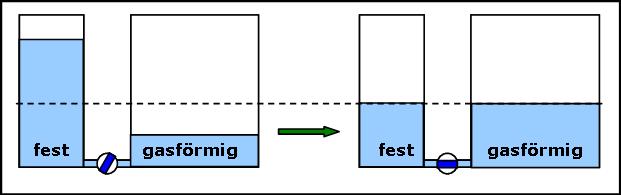

Die Entropie bestimmt die bis zu einer bestimmten Temperatur gespeicherte thermische Energie.

Durch die Analogie wird erkennbar, dass der Entropie durch die Definition der Temperatur der Charakter einer Speicherkapazität zukommt. Dies mag zunächst überraschen, weil zumeist die Thermokapazität* in dieser Rolle gesehen wird. Jedoch ist zu bedenken, dass die Thermokapazität als 1. Ableitung der Entropie alle Eigenschaften von seiner Stammfunktion erhält. Durch zahlreiche experimentelle Befunde wird zudem diese Deutung der Entropie bestätigt (s.u. 2. Verfeinerung und s. 5.2). Auch bei den drei Regeln des Regalmodells war schon angeklungen, dass die Entropie eine thermische Stoffeigenschaft ist, die die Größe des Speichersystems für thermische Energie beschreibt.

Bekanntlich haben feste Stoffe kleine Entropiewerte, Flüssigkeiten größere und Gase besonders große Entropiewerte (Querschnitte im Fluidmodell), wenn man alle Stoffe bei derselben Temperatur beurteilt. Das folgende Bild zeigt in einer einfachen Querschnittszeichnung eines Fluidmodells die Beschreibung einer Abkühlung eines festen Stoffes in einem luftgefüllten Raum. Wird der Hahn geöffnet und damit der thermische Kontakt hergestellt, so fliest die thermische Energie wie bei verbundenen Gefäßen solange bis in beiden Teilen der Modellapparatur die Füllhöhe gleich ist. Der feste Stoff kühlt sich ab, die Raumluft erwärmt sich. Die Endtemperatur/Füllhöhe liegt nicht beim Mittelwert der beiden Temperaturen, sondern näher bei der Anfangstemperatur des kalten Raumes. Die Gesamtenergie ist in diesem Beispiel konstant geblieben.

Das obige Bild visualisiert Rechnungen auf der Basis einer der Beziehungen:

Dabei bedeutet ΔQ die thermische Arbeit, die der heiße am kalten Stoff verrichtet, um die Temperaturänderung zustande zu bringen. In diese Näherungsrechnung gehen gehen außer den thermischen Stoffeigenschaften (Thermokapazität, bzw. Entropie) auch noch die jeweiligen Portionsgrößen, also die Massen oder die Stoffmengen der beteiligten Stoffe ein. Die Physik bevorzugt eher die spezifischen, also auf die Masse bezogenen Stoffeigenschaften, während die Chemie die molaren, auf die Stoffmenge bezogenen Varianten verwendet. Das einfache Fluidmodell kommt mit beiden Versionen zurecht, da Masse und Stoffmenge proportional zueinander sind.
Die Güte der Näherung hängt von dem Temperaturbereich ab, in dem das Verfahren stattfindet, und hierzu muss entweder der Mittelwert der Thermokapazität (linke Gleichung) oder der Temperatur (rechte Gleichung) verwendet werden. In alltäglichen Prozessen sind Entropieänderungen meist vernachlässigbar und die Thermokapazität wird als konstant angenommen.
Da Temperaturänderungen anstelle von Entropieänderungen einfacher zu messen sind, wird die erste Gleichung häufiger verwendet.
Mit dieser Grundversion lassen sich auch durchaus recht komplexe thermische Vorgänge beschreiben, wie sie z. B. in einem Kühlschrank ablaufen (in 6.4.2.).

Im Folgenden zeigen wir, dass man durch verschiedene Stufen der Verfeinerung dieses Modells die recht komplexen thermodynamischen Verhältnisse realer Stoffe sehr differenziert visualisieren und damit verständlich machen kann.

*(Je nach dem experimentellen Zusammenhang werden Thermokapazität und Entropie statt auf die Stoffmenge auch alternativ auf die Masse einer untersuchten Stoffportion bezogen, so dass man dann die jeweiligen spezifischen Werte von Entropie und Thermokapazität verwendet.)

Die 1. Verfeinerung

Entropie und Thermokapazität tragen beide zur Speicherfähigkeit von stofflichen Systemen bei, aber jeweils auf etwas andere Art. Der Unterschied lässt sich aber sinnvoll ins Fluidmodell integrieren:
Bei zunehmender Füllhöhe (Temperatur) steigt nicht nur der Bodendruck (Temperatur), sondern auch der auf die Seitenflächen. Je nach Bauart der Flasche (Stoffsystem) geben die senkrechten Wände mehr oder weniger nach, wodurch die Querschnittsfläche (Entropie) größer wird. Diese Zunahme stellt in diesem Modell die molare Thermokapazität dar, die ja - wie oben gezeigt - sich logarithmisch mit der Temperatur (Füllhöhe) ändert. Die unterschiedliche Größe des hydrostatischen Drucks auf verschiedenen Höhen unterhalb der Oberfläche des Mediums würde zu einer „bauchigen" Verformung der Seitenwände führen. Während im Grundmodell die Wände als starr angenommen wurden, berücksichtigt die erste verfeinerte Version des Fluidmodells dieses Phänomen. Allerdings wird statt der bauchigen Ausweitung die Verformung der Wände über alle Höhen gemittelt. Schauen Sie sich eine Visualisierung dieses Sachverhalts im Fluidmodell an:

Animation: Thermische Arbeit im Fluidmodell

Entropie und Thermokapazität beschreiben gemeinsam die Speicherkapazität eines Stoffsystems für thermische Energie, also der Energie, die auf den Energieniveaus eines Stoffsystems gespeichert werden kann. Dabei enthält die Entropie die Aussage über die Gesamtenergie, die vom absoluten Nullpunkt bis zur gerade aktuellen Temperatur des experimentellen Kontexts gespeichert wird, während die Thermokapazität die Änderung der Entropie im Verlauf der Temperaturskala, bzw. im Bereich der gerade aktuellen Temperatur angibt. Die folgende Animation verdeutlicht, dass das Fluidmodell gerade die quantentheoretischen Ergebnisse auf dieses Modell überträgt. Während der gezeigten Temperaturzunahme verdreifacht sich die gespeicherte thermische Energie, aber die Entropie nimmt nur auf das 1,5-fache zu. Der Radius des Modellzylinders sogar nur um das 1,2 fache:

Animation: Thermische Arbeit im Regal- und im Fluidmodell

Die 2. Verfeinerung

Beim Betrachten der vorigen Animation fällt der Farbwechsel des fluiden Mediums auf und er erfordert eine Erklärung, welches Phänomen dadurch dargestellt werden soll.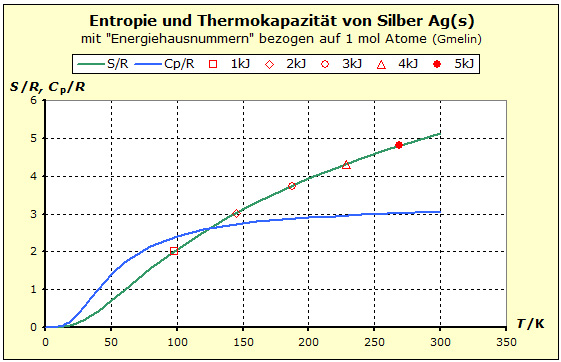

Wir betrachten dazu das obige Diagramm, das die Entropie- und Thermokapazität-Messwerte von Silber darstellt [s. 8.2/12 Gmelin-Handbuch].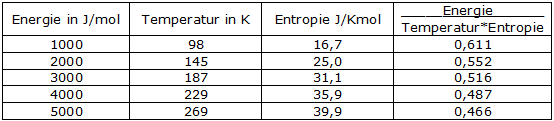
Die eingezeichneten "Energiehausnummern" auf der Entropiekurve rücken offensichtlich immer näher zusammen. Das erste Kilojoule gespeicherter Energie erbringt eine Temperatur von 98 K bei einer Entropie von S = 16,7 J/Kmol (S/R = 2,0). Das zweite Kilojoule verdoppelt diese Temperatur aber nicht, sondern führt nur zu 145 K bei einer Entropie von S 25,0 J/Kmol (S/R = 3,0), das dritte nur zu 187 K bei der Entropie von S = 31,1 J/Kmol (S/R = 3,74) , u.s.w.

Da der Quotient mit zunehmender Temperatur kleiner wird, muss man also feststellen: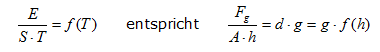

Das Produkt aus Entropie und Temperatur nimmt bei steigender Temperatur stärker zu als die gespeicherte Energie.

Nun entsprechen aber die Achsen im obigen Diagramm beim Fluidmodell gerade der Füllhöhe und der Querschnittsfläche und damit ergibt sich, dass wir dieses stoffliche Phänomen auf der Fluidmodellseite nachvollziehen können.

Bei normalen Flüssigkeiten gehen wir davon aus, dass die Dichte nicht von der Füllhöhe anhängig ist. Anders verhält es sich bei den ebenfalls fluiden Gasen: d = f(h), und zwar genau so, dass die Dichte mit zunehmender Höhe nach der Barometerformel abnimmt. Wenn wir uns unter dem fluiden Modellmedium jetzt ein dichtes Gas vorstellen, so können wir dem realen thermodynamischen Befund auch im Modell entsprechen. Wir vereinfachen jedoch auch hier, indem wir die Dichte über die gesamte Füllhöhe mitteln und diese mittlere (Speicherungs-)Dichte durch unterschiedliche Farbintensität im Fluidmodell darstellen.
Da wir das Fluidmodell im Zusammenhang mit dem Regalmodell entwickelt haben, konnten wir in der letzten Animation sowohl die Füllhöhe, die Querschnittsfläche wie auch die gespeicherte Energie quantentheoretisch berechnen und zeichnen lassen. Die Abnahme der Farbintensität war also nicht willkürlich, sondern entsprach genau den Quantengrundlagen.

Wir haben hier das Fluidmodell aus dem thermodynamischen Verhalten von Silber entwickelt. Es soll jetzt noch gezeigt werden, dass dies kein Sonderfall des Silbers ist, sondern dass es sich um allgemeines, thermisches Phänomen handelt.

Das Diagramm zeigt das thermische Verhalten einer ganze Palette von Feststoffen: eine polare molekulare Verbindung (H₂O), eine salzartige Ionenverbindung (NaCl), ein unpolares molekulares Elemente (Br) und ein Metall (Pb) [s. 8.2/12 Gmelin-Handbuch]. Man erkennt auch hier, dass die "Energiehausnummern" zunehmend näher zusammenrücken. Wir haben jetzt in diesem Diagramm die Achsen so gewählt, dass die Temperatur als abhängige Variable erscheint. Dadurch wird besser deutlich, dass es bei Stoffen mit großen Entropien mehr thermische Energie erfordert, um sie auf entsprechend hohe Temperaturen zu bringen, dass es sich also bei solchen Stoffen um thermisch träge Stoffe handelt. So wird Eis (1 mol Atome) mit der thermischen Arbeit von1 kJ auf 200K erwärmt, während man 1 mol Bleiatome mit dieser Arbeit nur auf etwa 70 K bringen kann und dass man mehr als 4 kJ benötigen würde, um nur in die Nähe von 200K zu kommen.

Die 3. Verfeinerung

Der Zylinder unseres Modellspeichersystems hat zwei Zuflussmöglichkeiten. Diese benötigen wir, um die beiden grundsätzlich verschiedenen Arten der Temperaturänderungen wiederzugeben:
Gemäß dem ersten Hauptsatz kann die innere Energie durch thermische Arbeit und durch mechanische Arbeit geändert werden. Weil es sich in beiden Fällen um Arbeitsvorgänge handelt, die entweder am System oder vom System geleistet werden, haben wir die Absperrhähne durch Symbole ersetzt, die einen Generator oder einen Pumpenmotor darstellen sollen.
Im oberen Fall hatten wir es mit thermischer Arbeit zu tun. Die thermische Energie wurde durch den seitlichen Zufluss in das System gebracht als der thermische Kontakt hergestellt war. Wenden wir uns nun der mechanischen Arbeit zu.

Auch die oben erwähnte Temperatursteigerung ohne Entropiezunahme läßt sich mit dem Fluidmodell darstellen. Bleibt die Entropie trotz Energiezufuhr konstant, so bedeutet dies im Modell, dass die Querschnittsfläche gleich bleibt. Die Wände geben also dem hydrostatischen Druck, der ja trotzdem mit der Füllhöhe steigt, nicht mehr nach. Sie werden also massiver und damit standfester. Dies wird hier durch zunehmende Intensität der Wandfarbe von hellgrau nach dunkelgrau symbolisiert.

Schauen Sie sich auch die Visualisierung dieses Sachverhalts im Fluidmodell an:

Animation: Mechanische Arbeit im Regal- und im Fluidmodell

Die Animation zeigt, dass alle Niveaulinien waagerecht parallel verschoben werden, dass also alle Besetzungszahlen gleich bleiben und nur die Niveauabstände größer werden. Als Folge dieser größeren Niveauabstände wird auch die blaue Halbwertsenergielinie länger, also die Temperatur höher. Wenn kein Teilchen das Niveau wechselt, ist das ein Zeichen dafür, dass bei diesem Arbeitsprozess keine elektrischen Wechselfelder mitwirken. Die Temperaturänderung mittels mechanischer Arbeit, Volumenarbeit, hat also andere physikalische Ursachen. Dieser andere Hintergrund macht es erforderlich, dass man thermodynamisch zwischen Volumenarbeit und allen Nicht-Volumenarbeiten unterscheiden muss.

Die beiden Grundvorgänge des ersten Hauptsatzes lassen sich natürlich auch mit dem Regalmodell allein darstellen. Es ist das grundlegendere Modell, dessen Berechnungen dann im Fluidmodell graphisch und anschaulich umgesetzt werden. Beide zusammen vermitteln einen sehr plastischen Eindruck von den thermodynamischen Phänomenen.

Die 4. Verfeinerung

Diese Verfeinerung führt uns auf ein den Hochschulen angemessenes Niveau. Atomare Gase können nach klassischer Vorstellung nur Translationsbewegungen in drei Raumrichtungen ausführen. Jedes Gasatom stellt drei Freiheitsgrade für die Speicherung thermischer Energie zur Verfügung, je einen in x-, y- und z-Richtung. Quantentheoretisch stellt ein Freiheitsgrad ein Eigenwertsystem mit unendlich vielen gequantelten Energieniveaus dar. Die energetischen Abstände dieser Niveaus folgen bestimmten Gesetzmäßigkeiten, in die die Massen der Gasatome, die zwischen ihnen wirkenden Kräften und die Größe des Raumes eingehen. (s. Abschnitt 2.4) Ein einzelnes Gasatom befindet sich zu einem bestimmten Zeitpunkt in jeweils einem dieser Zustände des x- , y- und z-Eigenwertsystems. Die Zustände in den verschiedenen Raumrichtungen können gleich oder unterschiedlich hoch angeregt sein.
Zu jedem Zustand gehört eine Raumfunktion, die etwas darüber aussagt, wie das entsprechende Atom über den gesamten Raum verteilt ist. Da man diese Funktion aus der zeitunabhängigen Schrödinger Gleichung ermittelt, ergibt sich, dass sie während der Lebensdauer dieses Zustands in unterschiedlichen Raumbereichen unterschiedliche Werte hat, die aber alle zeitlich konstant sind. Solche Zustände bezeichnet man deshalb als stationäre Zustände. Jedes Teilchen kann zu einem anderen stationären Zustand und einer anderen Raumfunktion wechseln, wenn entweder ein Photon emittiert oder absorbiert wird.
Das Verhalten von Teilchen in einem solchen Zustand macht deutlich, dass er nicht mit einem Bewegungszustand bei einer Ortsveränderung eines Teilchens kompatibel ist. Eine anschauliche Vorstellung über das unterschiedliche Translations-Verhalten eines Atoms in verschieden hoch angeregten Translationszuständen ergibt sich daraus nicht. Dennoch hat man die Bezeichnung "Translationszustand" beibehalten.

Bei den molekularen Gasen treten zwei weitere Speicherarten^* auf, die sich in ihren thermischen Eigenschaften auch deutlich von den Translationszuständen unterscheiden. Die Namensgebung dieser Speicher geht auf die klassische Vorstellung der Bewegungsmöglichkeiten von Rotation und Vibration zurück.
Bilden je zwei Gasatome Moleküle aus, so bleibt die Anzahl der Freiheitsgrade, also die Anzahl der Eigenwertsysteme für die Speicherung thermischer Energie erhalten (s. folgende Tabelle). Allerdings ändert sich die Abhängigkeit der Energieniveau-Abstände von der Teilchenmasse, den interatomaren Kräften und der Raumgröße.

In der klassischen Vorstellung können zweiatomige Moleküle um zwei Drehachsen rotieren und sie können gegeneinander schwingen. Die beiden Drehachsen liegen senkrecht zueinander und senkrecht zur Molekülachse, in der die Schwingung erfolgt.
Auf der Quantenebene hat man die Bezeichnung der Zustände in den zugehörigen Eigenwertsystemen als Rotations- bzw. als Vibrationszustände beibehalten, obwohl das messbare Verhalten dieser Zustände nicht gut mit den klassischen Vorstellungen von Rotation und Vibration kompatibel ist:
Eine Drehfrequenz ergibt sich nicht aus dem Verhalten in einem der stationären Rotationszustände, sondern aus den Übergängen zwischen zwei solchen Zuständen. Gleiches gilt für die Vibrationszustände. Auch hier sind diese Übergänge mit Emission und Absorption von Photonen verknüpft. Die Photonenfrequenzen können als Dreh- bzw. als Vibrationsfrequenz gedeutet werden. Zu jedem Eigenwert gibt es auch hier eine zeitlich konstante Raumfunktion, die sich nicht als stehende Welle deuten lässt:
Außer an den Knotenpunkten haben stehende Wellen im gesamten Raum keine zeitlich konstanten Amplituden.

* Auf die Implementierung einer vierten Speicherung, nämlich der Speicherung thermischer Energie in den Elektronenzuständen, wird hier verzichtet, weil sie bei den meisten Stoffen keinen Beitrag zur Entropie und damit zum thermischen Verhalten der Stoffe beisteuert.

Damit haben wir drei unterschiedliche Arten von Speichern für thermische Energie kennengelernt und wenden uns jetzt dem Zusammenwirken dieser Speicher in verschiedenen Fällen zu, d. h. wir konzentrieren uns jetzt auf das Verhalten der molekularen Gase zunächst bei thermischer Arbeit und dann bei Volumenarbeit. Als Beispiel für ein molekulares Gas nehmen wir Bromdämpfe erwärmen sie mit thermischer Strahlung (aus einem Brenner oder von einem elektrisch beheißtem Draht) von der Standardtemperatur bis auf 500K. Die beiden folgenden Bilder zeigen die drei Speichersysteme im Fluidmodell, links bei Standardtemperatur und rechts bei 500K. Die Basisleitung verbindet die drei Speicherbehälter, so dass sie sich physikalisch wie klassische, verbundene Gefäße verhalten.

Erwärmung von Br₂(g) durch thermische Arbeit

Man erkennt leicht, dass in allen drei Speichern der Pegelstand, also die Temperatur, sowie die Menge an fluidem Medium, also thermischer Energie, größer geworden ist. Schwieriger ist es zu sehen, dass auch die Entropie, also die Querschnittsflächen, zugenommen haben. Am besten ist es noch am Vibrationsspeicher zu erkennen, da hier die Fläche sehr klein und damit die Zunahme prozentual recht groß, ca. 75%, ausfällt. (Translation +5,4%, Rotation +5,9%) Die Darstellung wurde vom Thermulation-II Programm berechnet und man muss bedenken, dass durch die Auflösung des Bildschirms bedingt, die prozentuale Veränderung eventuell unter einem Pixel bleibt, so dass der Bildschirm sie nicht anzeigen kann.

Erwärmung von Br₂(g) durch Volumenarbeit

Auch hier erkennt man, dass Temperatur und thermische Energie in allen drei Speichern zugenommen haben. Zu erwarten wäre eigentlich, dass sich die Volumenarbeit nur auf den Translationsspeicher auswirkt, weil nur diese Eigenwerte vom Volumen abhängen. Allerdings würde sich durch eine Volumenarbeit dann im Translationsspeicher eine andere Temperatur einstellen als in den beiden anderen Speichern. Da das schwer vorstellbar ist, sollten wir einen Mechanismus suchen, mit dem die thermische Energie vom Translationsspeicher auf die beiden anderen übertragen wird.

Im Detail wenden wir uns dieser Frage erst im nächsten Kapitel über die spontane Emission zu. Wir haben aber hier schon auf die Bedeutung der Photonen hingewiesen, die stets auftreten, wenn Teilchen ihre Niveaus wechseln, deshalb können wir hier schon das Grundsätzliche verstehen:
Steigt die Temperatur im Translationsspeicher, so setzt dort eine erhöhte Emission von thermischer Strahlung ein. Dieser stärkere Photonenstrom gelangt im Fluidmodell durch die Basisleitung zu den Rotations- und Vibrationsspeichern und bewirkt dort, das Teilchen auf höhere Niveaus wechseln, solange bis sich dort die gleiche Temperatur eintstellt wie im Translationsspeicher, der der Angriffspunkt der Volumenarbeit war. Bei gleicher Temperatur halten sich Emission und Absorption in allen Speichern das Gleichgewicht. Die vom Programm berechneten Änderungen der thermischen Energie durch die Volumenarbeit sind im Rotations- und im Vibrationsspeicher bis auf Rundungsabweichungen die gleichen wie im Fall der thermischen Arbeit.

Wir sehen hier einen Unterschied zwischen idealen und realen Gas: Während im idealen Gas bei Volumenarbeit die Entropie trotz Temperatur und Energiezunahme konstant bleibt, steigt im realen Gas auch die Entropie, weil durch die "Fluidität" der Photonen die thermische Energie, die mittels der Volumenarbeit nur dem Translationsspeicher zugeführt wurde, auf die anderen Speicher übertragen wird. Die innermolekularen Freiheitsgrade machen das Bromgas zu einem realen Gas.
Durch die thermische Arbeit stieg im hier behandelten Beispiel die Entropie um 7,5% und durch die Volumenarbeit um nur 3,2%.