In combinatorics, one distinguishes between macro- and micro-states. An ensemble of a certain number of particles with a certain total energy can realize different macro states in a certain eigenvalue system. These can be distinguished from each other by macroscopic measuring methods by their different behavior and thus identified.
Among all the macro states of a given particle number, total energy, and given eigenvalue system, there is one which could realize a maximum number of micro states by a special distribution of the particles on the energy levels of the eigenvalue system. This distribution is called the dominant distribution, and this macro-state is called the dominant macro-state
This formula is used to calculate the number of microstates W in a system. If, in a first arrangement, the "energetic places" of two particles are exchanged in the shelf model or on the energy levels of the system, a further microstate is obtained which the system could realize and which macroscopically would behave completely identical , ie chemically and physically, as the original state, because during the interchanging the particle number, the total energy and the energy distribution remain the same. Many micro states may belong to macrostate. However, since all microstates behave in the same way, no measurement can determine which microstate of a system is actually realized.

Scientifically exact, the entropy is defined as the natural logarithm of the number of all microstates of a dominant distribution, that is, of a dominant macrostate. In natural systems, however, these numbers are so large that it is not possible to visualize them clearly. Even for the element with the smallest molar entropy, for the diamond, at standard conditions for 1 mol of carbon atoms 10^7,48.1022 states are obtainable.

Since numbers of this size escape any intuition, such futile attempts at illustration are dispensed with.
However, the number of microstations increases with the number of occupied levels, and these numbers lie in areas that we can imagine well. The following figure shows that the correlation between the number of micro states and the occupied levels applies not only to the shelf model for small particle numbers, but also to real large mass fractions. Thus, the numbers of the occupied levels for one mole of helium or argon are on the order of 10³ at standard conditions, and the noble gases are elements with relatively large entropy. It is also shown in the model that this correlation is independent of the respective substance, ie, the respective level distance.

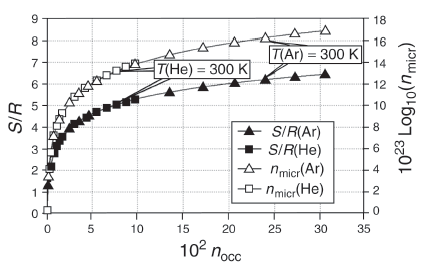
The description of the entropy as a measure of the number of occupied levels represents a reasonable simplification. It also seems plausible to correlate the size of the energy storage system with the number of levels on which the "energy packets" are stored. A concrete example, where the relationships described here are explained using the shelf model, can be found in chapter 2.3