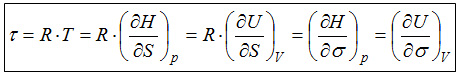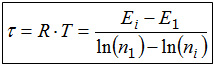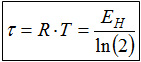Let's have a look to some examples that demonstrate how the basic rule is to be used. In the following picture you see three shelves.

In these three cases there are:     9 particles bearing 9 energy units

Nevertheless, only the shelves-figure on the right side is of any importance. The number of occupied energy levels is greater than in the other cases and the four lowest levels are concerned. The number of occupation decreases with increasing height of the energy level, similar to the Boltzmann-distribution. Arrangements proved to be very unlikely in which a higher level holds an greater number of particles than a lower one does, as shown in the left figure.

All three distributions show macro states (see explanatory notes to the basic rule) in which the total energy and the number of particles are the same but differ in the distribution of the energy to the given levels (corresponding to a given substance type). In the left shelf, a macro state is shown, to which there are 503 micro states, already 1686 micro states in the middle and at last the dominant distribution with 3790 micro states on the right. It is the dominant macro state for these 9 particles in this energy eigenvalue system and the given total energy of 9 energy units eu.

Entropy is to be calculated by the following law:

Entropy fits the equation S = R ^. ln(W), which is going back to Ludwig Boltzmann. Because changes of entropy could only come from the term ln(W) and naturally not from the gas constant R it is reasonable to define only ln(W) as fundamental entropy σ like KITTEL and KRÖMER suggested. One of the advantages reached by this specification consists in the change of the unit of entropy. The unit of the conventional entropy S, which was J/K, had been the main reason for all misinterpretations of the entropy phenomenon, because the relation of entropy and the number of microstates was not transparent. However entropy σ = S/R is a mere number, the quality of which is best described by the unit mol.

Another advantage follows from the relation of entropy and temperature. As well the temperature phenomenon can be described considerably clearer by the specification of KITTEL and KRÖMER concerning the fundamental temperature τ = RT. This will be illustrated in the following section.

If the particles of a system / substance are transferred from lower to higher energy levels, this changes the temperature of the system. The number of occupied levels and thus the entropy increase.
Left:
low temperature,
8 occupied levels,
low entropy
Right:
high temperature,
10 occupied levels,
high entropy.

1. The definition of temperature T (or fundamental temperature τ= RT) given by the classical thermodynamic:

(R: gas constant; p: pressure ; V: volume;
H: enthalpy ; U: internal energy ; S: conventional entropy ; σ fundamental entropy ; )

2. The definition of temperature T (or fundamental temperature τ= RT) given on the basis of quantization of energy :

(R: gas constant; E_i : energy of level i; E₁ : energy of level 1;
n₁ : occupation number of level 1; n_i : occupation number of level i)

A comparison of the two definitions shows that in both cases a quotient occurs. Because in both cases the numerator is a difference of energy values, we conclude that also the denominator indicates an equal quality in both cases. From the second definition it is clear that this quality is a difference of numbers. Of course the values of the "occupation numbers" must be natural numbers, because it is not possible to store only one half of a particle on the energy levels. The quality of a number is not lost by the logarithm. If the intensity phenomenon 'temperature' is described by RT* this would as well be indicated by the unit kJ/mol, because all intensive properties are described by quotients.

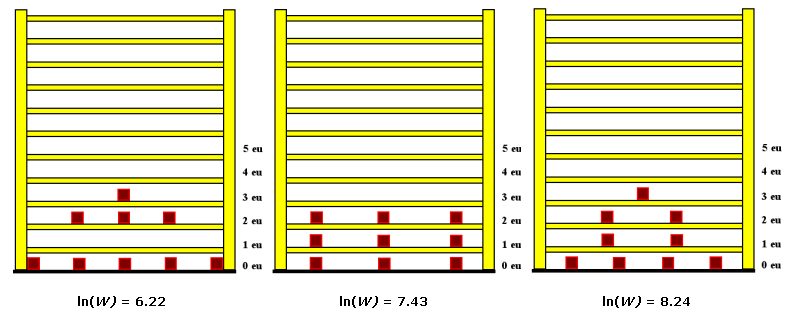
The stored energy is related to the numbers of microstates, which are accessible for the system or substance having that certain amount of stored energy. Under common temperature conditions the number of microstates is so immense that no human being is really able to get a vivid perception of such a number. For 100g common salt or 10 liters of Helium the values lie in the order of magnitude of: 10^3.1024.

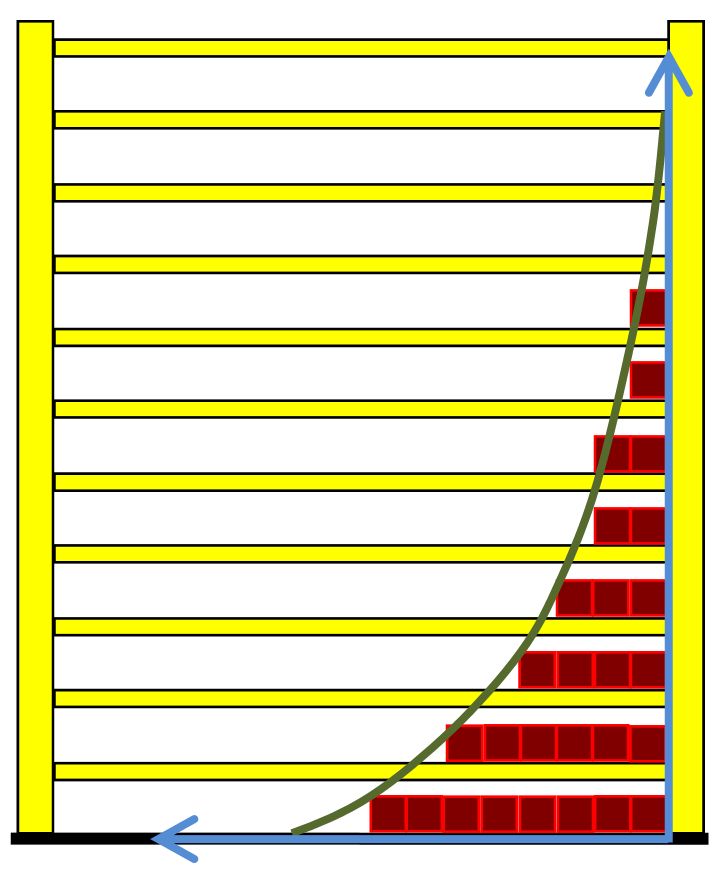
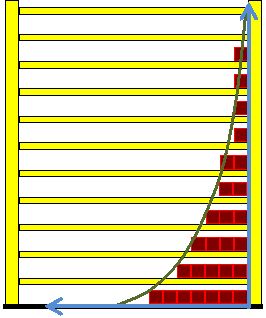
The number of microstates is strictly monotonic increasing with the number of occupied energy levels. So it is a correct simplification to say: entropy is a measure of the number of occupied energy levels. And at the same time this is a wise simplification because the number of occupied levels lies in a comprehensible order of magnitude. For 10 liters of Helium we find about 2000 occupied levels.

A mathematical peculiarity of the exponential function can be used to simplify the thermodynamic definition of the temperature on the basis of the energy quantization. This special feature is that, after constant changes of the independent variables (here the energy), the function values halve in half. This property is well known from the radioactive decay, where it is used to characterize the speed of the decay: since the independent variable for radioactive decay is the time, the half-life characterizes this phenomenon. In complete analogy, one can speak of the half-energy E_H, ie, the additional energy distance E_i - E₁ at which the occupation number n_i of a level is halved in comparison to lowest level n₁.

E_H = E_i - E₁
n_i /n₁ = 0,5   ⇒   ln(n₁) - ln(n_i) = ln(2).

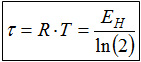
*(The difference between the Boltzmann constant k and the gas constant R consists only of one unit change. Correctly, in the case of unit conversion, a numerical value and a unit symbol should appear on both sides of the equality sign: 1 mol = 6,02214 ^. 10²³ co. (Here, the unit symbol 'co' stands for 'countable objects'.)
This yields: k = 1,38066 ^. 10^-23 JK^-1co^-1 = 8,31453 JK^-1mol^-1 = R.
For the understanding of the thermodynamic relationships, it does not seem to be helpful to change the symbol for the quantity value when changing a unit, since quantity values are independent of the units used. )