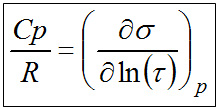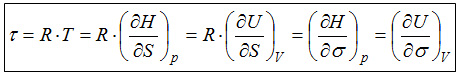3. The Fluid Model

In chapter 2 it was shown how the storage of thermal energy can be understood on a quantum theoretical basis.

In the following chapter we will show that there is also a classical mechanical analogue to this storage process which makes use of the properties of fluid media. However, the dimensions of the mechanical storage shown for this fluid medium were calculated quantum theoretically with the shelf model. These are, therefore, "classical" transformations of quantum theoretical results. Also, this model provides analogies for the thermodynamically relevant phenomena as temperature, thermal energy, entropy and thermal radiation.

The correlation of entropy and thermal capacity is illustrated with an excursus into the theory and clarified with animated graphics. Entropy and thermal capacity, as the first derivative of entropy, determine the size and size changes of the thermal storage systems belonging to the great variety of its substances that nature provides us with.


3.1. The Theoretical Fundamentals of the Fluid Model

The thermodynamic relationship between the molar entropy σm and the molar thermal capacity Cp can best be seen in the relationship given below
(Nomenclature s. 1. und 2.3):

Cp-Formel
Substantiation of the Cp-formula

Since the logarithm function is monotonically increasing, the term ln(τ) also increases with increasing temperature. If the entropy σ is semi-logarithmic against the temperature, the thermal capacity can be determined as the slope (first derivative) in this diagram.
However, the entropy increases with increasing temperature only when the energy is supplied to the system by thermal work ΔQ. If the temperature increase is achieved by performing mechanical work ΔW (for example, when compressing a gas), the entropy remains constant despite the rising temperature.

Thermodynamics distinguishes four types of quantized energy storage. Because the chemical substances have four kinds of eigenvalues, there are also four types of energy stores, which belong to four types of energy states: translational, rotational, vibrational, and electron states. They behave differently when thermal or volume work on the substances is carried out. The fluid model is capable of adequately visualizing the different behavior, because it is able to convert quantum-chemically calculated values of the individual memories graphically. The Thermulation-II program calculates these values from the known spectroscopic data and can output these as numerical values, as Boltzmann distributions and as fluid model diagrams.

Thermodynamically, the temperature is defined by the relation given below.

Temperaturdefinition

A vivid idea of this definition is obtained by the following storage analogy:

If a fluid medium is filled into a cylindrical vessel with the cross-sectional area A, the hydrostatic pressure p increases at the bottom of the cylinder because the weight Fg of the liquid that has been filled in increases. The storage of thermal energy behaves completely analogously to this storage of a fluid medium.

Zylinderflasche

It corresponds:

the weight of the fluid medium Fg      ----------    the thermal energy H resp.U
the cross-sectional area A                 ----------    the entropy S resp. σ
the hydrostatic pressure p                 ----------    the temperature T reps. τ.

Because of the linear relationship between the pressure p and the filling height h, the temperature-analogous variable can also be read off at the filling level.

To prove this we show that the hydrostatic pressure phyd is defined analogously to the temperature: S-Analogie

The outlet line - possibly with a tap - represents the (thermal) contact to the environment or to other substances. A closed tap would mean perfect thermal insulation.