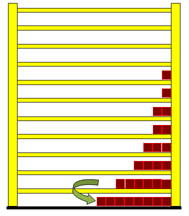
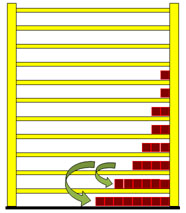
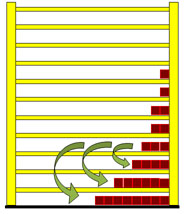
Dealing with the radiation law you easily find out, that Max Planck developed this law from entropy considerations, but how the train of thought was actually led, is rarely described. With the shelf-model however it is not difficult to reconstruct it in its fundamental courses and so it is to be introduced here right now.

If a particle in the shelf changes from a higher to a lower level, it radiates light. The frequency of the light (photon) depends on the distance between the two levels.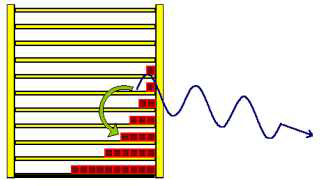

In this case the photon is equivalent to 3 energy units.

Particles from the other levels can make "quantum transitions" downward as well, and radiate different number of energy units. In the next picture a quantum transition of 4 energy units is drawn. With larger energy the frequency of the light becomes larger and the wavelength will be smaller.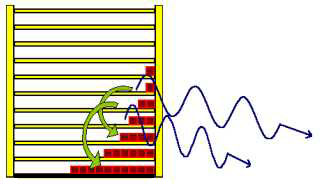

The second wave train has a shorter wavelength.

Understandably the particles from the lowest level cannot radiate any light, because they are not able to carry out a quantum leap downward. The particles from the first level can radiate only one frequency, those from second however two frequencies, which correspond to one, and/or two energy units. The higher the level of the jumping particles the greater the number of frequencies they may radiate. The three next pictures illustrate this.

Now we are able to calculate a simple case completely. As example we take the situation of 30 particles with 43 energy units distributed on seven levels.

Video with soundtrack: Calculation of an Emission Spectrum

A supplement should be added about the idea of this calculation. Before each evaluation of the number of transitions, it is assumed that all particles are always present in the same distribution. This means that before each quantum leap, the temperature is always the same, and all the particles that have previously jumped downwards are raised to their old level by a separate process. This, of course, also corresponds to the phenomenon when the emission spectrum of a substance is observed at a certain, constant temperature. Since the thermal radiation corresponding to this particular temperature can not be prevented, the corresponding Boltzmann distribution is kept constant by this radiation, as long as the radiating substance is in an isolated system.

The next diagram shows the spectrum calculated in the video again.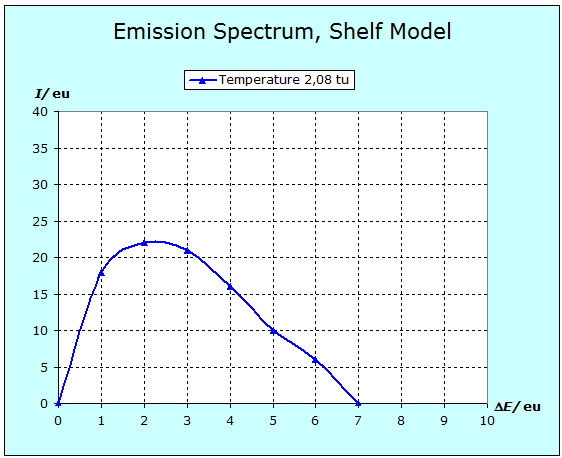

Now this spectrum is still very imperfect and rough. But if the same kind of calculation is carried out for 1000 particles by a computer a much smoother curve results: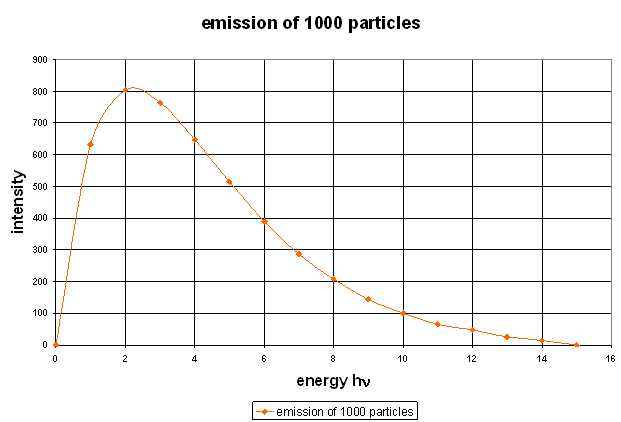

As next step we can calculate spectra for different temperatures in the shelf model. A curve family results, which is very familiar since it is published in connection with the Planck radiation law in numerous text books. With a constant number of particle and increasing temperature the maximum of the spectrum slides to higher energy/frequencies and at the same time the intensity increases. This Shelf Model property corresponds to Wien's displacement law.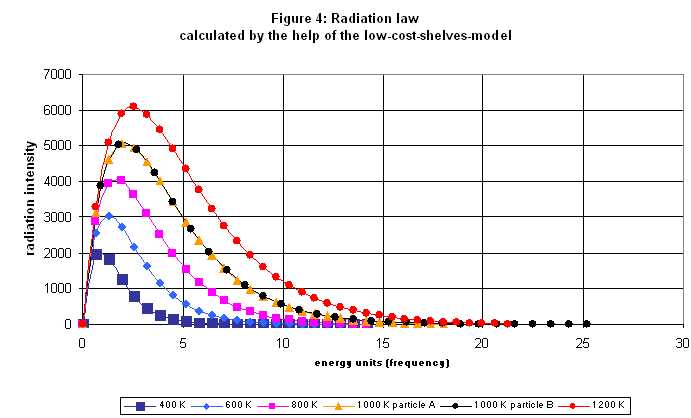

Have a look at the two curves calculated for the temperature of 1000 K. They had been computed for two different kinds of substances/particles. You recognize this by the fact that the level spacing is different. With the particles A the level distances are smaller than with particles B (orange triangles for A, black dots for B). Nevertheless the two curves are completely identicle. Thus it can be understood that actually all materials show the phenomenon of the red glow at approximately the same temperature. Let us for example assume, the frequency of red light in our model would correspond to 5 energy units and we heat up the materials A and B slowly. The radiation intensity increases homogeneously with both and as soon as it reaches an amount that our eyes are able to notice it, we see red glow with both materials