6. Experiments I :
Thermal Properties of Matter

In the context of quantum thermodynamics, it seems sensible to classify the experiments according to aspects which are based on the changes in the substances under investigation on the quantum level.

In this sixth chapter, we start with such experiments in which only the occupation numbers of the energy levels change within the energy storage systems, while the level distances remain the same. Transferred to our everyday language it means that we look at processes where the temperature changes but the substance remains essentially the same. We compare the thermal properties of different substances in processes like heating, cooling and temperature equalization. Doing so, we have to carry out the experiments in such a way that aggregate state changes do not occur.

Furthermore, we investigate changes of the energy level distances while the occupation numbers remain the same. In spite of the changes in the energy level distances, the substance remains the same in this particular case while the temperature changes.

From these experiments, we will see how knowledge about the thermal radiation contributes to the understanding of the thermodynamic drive and the relationship between the entropy and the thermal inertia of a substance.

In order to view the video clips of the experiments, the Flash player must be installed on your computer.

If work in a physics sense is performed on a substance, the energy state of the substance changes. This process is commonly referred to as work in a scientific sense and the type of process can be described by means of adjectives such as electrical, mechanical or the like for a more precise definition.
Under thermal work, only such a process is to be understood in which the state of the energy stored in the quantized levels of the object changes in a certain way. This type of energy is called thermal energy. For an introduction to this chapter, please watch the following video:

Video with soundtrack: Thermal work and photons

The decisive criterion for the fact that an operation receives the attribute "thermal" consists, therefore, in the constancy of the entire quantized energy storage system, or, as quantum theoric, the maintenance of the eigenvalue system. All energy levels remain the same, but the occupation numbers change.
Furthermore, it is characteristic of the thermal work that such processes are not possible without changes in entropy. By contrast, changes in temperature, thermal total energy and possibly pressure can also result from mechanical operations without the total entropy changing. In Section 6.2, we shall deal with such questions.

The experiments we are discussing in this chapter are all without changing the eigenvalue system. It is therefore a question of processes in which the substances are retained, but their temperatures are altered: heating, cooling, temperature equilibrium between two substances at the beginning of different temperatures. Our goal here is to get to know the thermal properties in the experiment and to develop a basic understanding of the thermodynamic drive.
Aggregate state changes and chemical reactions are, of course, excluded here because the eigenvalue system changes. These are examined in the next chapter.

In section 3.2, we have already dealt with the fact that the entropy of a substance at a temperature T is linked to the amount of energy that is needed to heat the substance from the absolute temperature zero point to the temperature T. However, since this overall energy is not accessible to us by simple means, the following experiments are designed in such a way that we can see what effect this total energy has on the thermal behavior of a substance at any temperature. If we heat two substances of different total energies with the same amount of thermal energy, we can examine whether they behave differently in the ratio of their entropies.

In the concrete planning of such an experiment, however, questions arise that must be considered:

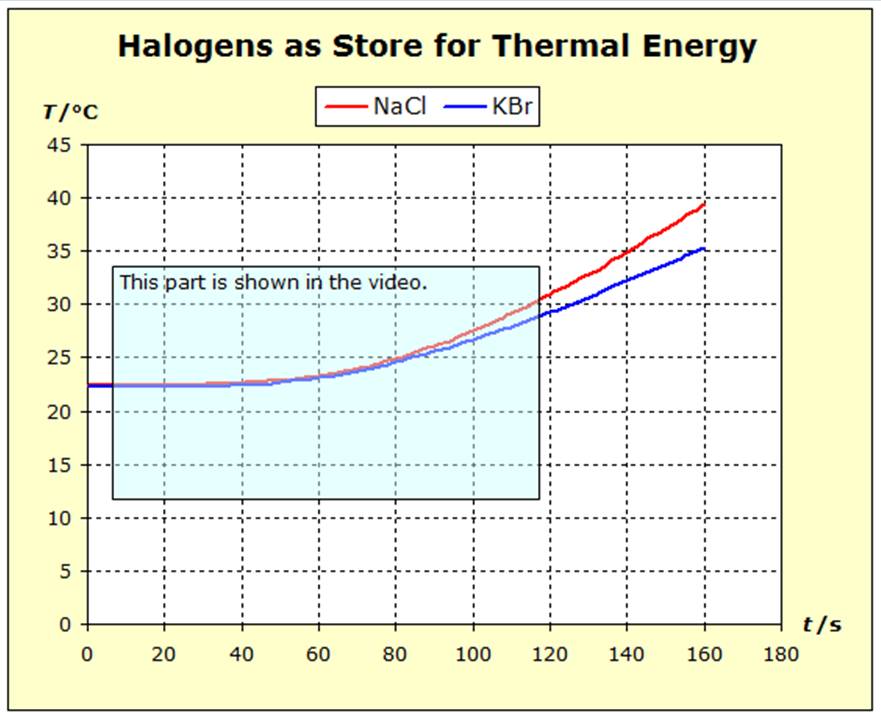
From the following figure it can be seen that two test tubes are placed in two electric heating blocks which are filled with two small-crystalline sections of material so that the fillings are flush with the upper edge of the heating blocks. In the left heating block, sodium chloride should be heated, in the right potassium bromide.

From the considerations of the atomic entropy (see Section 5.2), the same energy supply should be applied to the same atomic numbers. So we have to consider the different densities of the two substances. In the left test tube a quantity of n(NaCl) = 75.2 mmol of sodium chloride and in the right test tube n(KBr) = 47.1 mmol of potassium bromide are heated.
In order that the energy supply per atom - or more precisely per ion - is the same in both substances in equal time intervals, we have to control the two heating blocks with different current intensities at the same voltage. Since the current intensity I enters into the power P squarely, it can easily be calculated that in our experiment for the sodium chloride a current intensity which is about 26% higher must be set. The temperature measuring probes were centered with the aid of silicone discs to ensure that they are located in the center of the test tube and therefore are at equal distance from the heating wires.
After these preliminary considerations, you can now watch the video of the experiment.

Video: Thermal work executed to halogenides

After the voltage is switched on, the heating blocks are first heated and after about 25 seconds the centrally placed temperature measuring probes react to the thermal energy supplied.
The experimental results show that an equal energy supply for the sodium chloride results in a higher temperature increase than in the case of potassium bromide, which thus proves to be the thermally inert substance. Looking at the entropy values of the two substances, one finds that the molar standard entropy is smaller for sodium chloride than for potassium bromide:

S(NaCl) = 72.13 J/(Kmol)   or   S/R = 8.68

  S(KBr) = 95.90 J/(Kmol)     or   S/R = 11.53

This value is comprehensible both from the force and the mass rule:
In sodium chloride, the bond distance is significantly smaller than in the case of potassium bromide, since both the anion and the cation have a smaller number of shells in the atomic shell. Thus the restoring force in the NaCl bond is stronger, the corresponding energy level distances are greater and this results in a smaller entropy contribution. In the sodium chloride mass and force control act in the same direction. Because the masses of both ion species are smaller, this results in a smaller entropy contribution. Less levels are occupied in sodium chloride and so the supplied energy must be distributed to fewer levels. Thus, with less energy an equal temperature increase or with the same energy a larger temperature increase can be achieved.

* If you would like to find out more about the "thermal inert" property, please refer to the following link:    To define thermal inertia

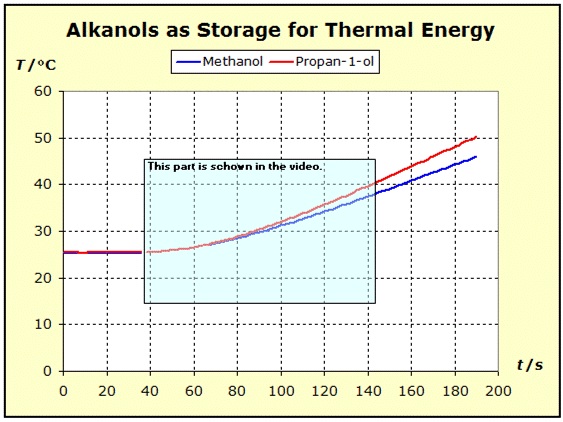
If the thermal properties of substances with different stoichiometry are to be compared, it has already been pointed out in section 5.2 that it is expedient to consider the values of the entropy and heat capacity, in relation to the number of atoms. The importance of the atomic entropy will be explained here by a simple example.
A gas consisting of individual nitrogen atoms has an entropy value of (standard conditions):

S^T(1mol N) = 141.6 J/K      or   S^T/R(1mol N) = σ^T(1mol N) = 17.03 = σ_tot(1mol N)

Since these individual atoms would neither be able to rotate nor to vibrate in the gas, only the levels of the translational states would be occupied in this gas. The program Thermulation-II shows that this one mole of N atoms is distributed to 4260 levels. We assume three eigenvalue systems - one each in the x, y, z direction - on the levels of which 1 mol of N atoms are distributed. In each direction 1420 levels are occupied: 3x1420 = 4260. The above entropy value results from this distribution.

If N₂ nitrogen molecules are formed from this portion, the mass of the particles occupying the corresponding translational levels is doubled, but the number is halved. According to the mass rule, the level differences would thereby be reduced and then half the number of particles distributed at these narrower levels. However, these 0.5 mol N₂ molecules occupy not only the three eigenvalue systems of the translation, but also two eigenvalue systems of rotation and one system of vibrations. The Thermulation-II program calculates the following values:

σ^T(0.5mol N₂) = 9.03      σ^R(0.5mol N₂) = 2.82      σ^V(0.5mol N₂) = 0,00

σ_tot(0.5mol N₂) = 11.85

The two σ_tot values represent comparable values of the thermal inertia of nitrogen atoms and nitrogen molecules because they refer to equal numbers of atoms. We simplify now the spelling of atomic entropies:

σ_at(N) = 17.03      σ_at(N₂) = 11.85

In many everyday cases, however, a good estimate of thermal material properties is desired, and this can be easily achieved by forming the atomic entropies S_at or S_at/R = σ_at from the tabulated standard entropies by dividing the standard entropies by the number of atoms of the corresponding molecule type.

The next experiment shows the thermal properties of methanol and propan-1-ol in comparison. In the interpretation of the experimental results, the atomic entropies of these two compounds help us very well to understand the cause of the thermal behavior via the force and mass rules and the atomic structure of these two substances.

The measuring apparatus (see picture below) is constructed similarly to the previous experiment. The current and voltage measurement is carried out directly on the DC power supply. Here, too, the current intensity is set so that both substances per atom receive the same energy supply per unit of time.

Video: Thermal work on primary alkanols

The experimental results show that an equal energy supply to propan-1-ol results in a higher temperature increase than in the case of methanol, which thus proves to be the thermally more inert substance. If one considers the entropy values of the two substances, it follows that the molar standard entropy is smaller for methanol than for propan-1-ol:

S(CH₃OH) = 126.8 J/(Kmol)     or   S/R = 15.25 = σ(CH₃OH)

S(C₃H₇OH) = 192.9 J/(Kmol)     or    S/R = 23.2 = σ(C₃H₇OH)

From these values, however, the thermal behavior of the two substances of the experiment shown above is not readily understood. However, if we calculate the atomic entropy values from the two values, the image changes:

S_at(CH₃OH) = [126.8 J/(Kmol)] : 6 = 21.13 J/(Kmol)    or   S_at/R = 2.54 = σ_at(CH₃OH)

S_at(C₃H₇OH) = [192.9 J/(Kmol)] : 12 = 16.05 J/(Kmol)    or   S_at/R = 1.93 = σ_at(C₃H₇OH)

Now, as in the previous experiment, the halides show that the substance with the greater entropy value is the thermally more inert material. This can also be understood from mass and force rules. The average atomic mass of the methanol is 5.33 g/mol and for propan-1-ol it is 5.00 g/mol. The larger mass provides a greater entropy contribution in the case of methanol than in the case of propan-1-ol.

Since, however, the molecular surface is smaller in methanol, the van der Waals forces - and thus the corresponding energy level distances - are also smaller in methanol, and therefore contribute more to entropy than to propan-1-ol.

We can now even compare the behavior of the salts with those of the alkanols, if we also represent the entropy of the halides as atomic entropies:

S_at(NaCl) = [72.13 J/(Kmol)] : 2 = 36.07 J/(Kmol)   or    S_at/R = 4.34 = σ_at(NaCl)

S_at(KBr) = [95.90 J/(Kmol)] : 2 = 47.95 J/(Kmol)   or    S_at/R = 5.77 = σ_at(KBr)

Let's try a rough estimate. For this we dispense with the differentiation between the two salts and the two alcohols and take the respective mean values as points of reference and we analyze the four measurements as follows:

n(NaCl) = 150.4 mmol ions;          n(KBr) = 94.2 mmol ions;      n(meanvalue) = 120 mmol
n(CH₃OH) = 443 mmol atoms; n(C₃H₇OH) = 480 mmol atoms; n(meanvalue) = 460 mmol

σ_at(salts) = 5 (approx.)
σ_at(alkanols) = 2.2 (approx.)

The experimental data were:
Salts:             Δt = 100s;                     ΔT =   7K;         I = 2.5A
Alkanols:        Δt = 100s;                     ΔT = 13K;         I = 1.5A

Although the apparatus and the measurements were simple, the results of the measurements are consistent with the material specifications and the salts confirm themselves as the thermally more inert substances compared with alkanols.
The interpretation of the atomic entropy as a measure of thermal inertia appears to be very promising, especially when referring to the quantities of substances with the same particle numbers.

If you execute thermal work on a material by heating it up, it expands. In this case, the substance again performs mechanical work to its environment, if this does not consist of the pure vacuum. The substance performs volume work. For most substances, the energy conversion associated with this work is negligible because the expansion is very small. The gases, however, are an exception in two respects: the expansion is not negligible, and all gases expand by practically the same factor.
The video shows two examples: expansion during the heating of 50 mL air and 50 mL helium in a gas syringe. The heating source is a hairdryer.
Watch the video.

Video: Heating different Gases

The picture below shows the measured volume change of air and helium with increasing temperature. For comparison, the V(T)-function of the ideal gas was plotted.

It can be seen that after a certain initial phase, both measuring curves are parallel to the ideal gas curve. The same extension, which points to the Avogadro hypothesis as an interpretative approach, becomes evident here.
From a quantum thermodynamic point of view, several effects are superimposed here:
The hot hair dryer emits more thermal photons than the room air and causes gas particles to change their levels so that the half-value energy increases. At the same time, the gas carries out mechanical work on the environment during volume expansion. When the volume is increased, the quantum theoretical eigenvalues are brought closer together and the half-value energy decreases, without an additional level change of the gas particles.
As a result of the thermal work done by the hair dryer, the thermal energy in the material increases as the particles change to higher levels. The simultaneous volume work which the gas executes to the environment, causes that the thermal energy decreases, because the distances between the energy levels with all particles on them decrease.
At constant volume, a similar thermal work results in a greater increase in temperature. Under a constant volume, the gas is thermally less inert than at constant pressure. In this experiment, it becomes clear that the thermal capacity between C_p and C_V must be differentiated, that is to say whether one is operating at a constant volume (and not constant pressure) (C_V), or whether pressure equilibrium with the environment can take place (C_p). The pressure compensation was therefore pointed out in the video.

Since the Flash-Player is synonymous with the playing time of the video, you could also create these corresponding measuring tables or diagrams. This was not done here, but still a reference in this direction is indicated. In the case of normal air the temperature increase started 7 seconds after turning on the hair dryer. In the case of helium it was already after 4 seconds.
The measuring probe is located in the middle of the gas chamber, the thermal energy of the hair dryer comes from below and has to go a certain distance up to the measuring probe. Thus, an influence of the thermal conductivity of helium and air will also be expected, which makes the "delay" of the display comprehensible.