In publications and thermodynamic tables, not only the standard values of enthalpy and entropy of the formation reactions are listed, but also values for the reaction enthalpies of specific reactions, such as combustion reactions. At the same time, reaction enthalpies of this type are referred to as combustion enthalpies or calorific values in analogy to the formation enthalpies of individual substances. For example, the reaction equation for the combustion of natural gas is given here:

If such values are then used for the assessment of a substance such as natural gas as a primary energy carrier, this approach raises questions: Is the substance natural gas an energy carrier? Who carries what energy? What are the energetic functions of oxygen and / or the resulting products in combustion?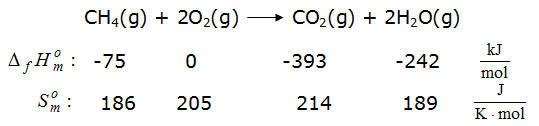
In order to answer these questions we want to pursue and comment on the next steps that are taken in classical thermodynamics in order to get the combustion enthalpies.
Step 1:
Below the reaction equations are written the values of the molar standard formation enthalpies and the molar standard entropies.

Step 2:The sum of these values is formed on both sides, after weighing them with the respective stoichiometric numbers ν.

This step urgently requires a comment with regard to the questions posed, since these values express the influence of all the substances involved. On the other hand, this value no longer depends on whether it was formed from two or more substances. He could as well represent only one substance. The values on the reactant side characterize the thermal properties of the reactants and those on the product side correspond to those of the products. Illustratively, one can say that the sum values of the reactant side represent a mean value with imaginary mean value particles and the sum values of the product side characterize in the same way a developing fictive end product. This view also appears to be justified because all reactions in which the values for the reactant and product side are the same behave thermodynamically equivalent.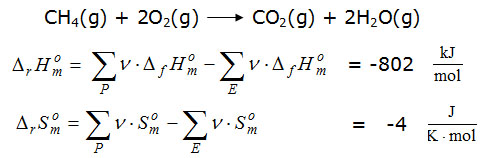
Step 3:
The differences of these values are formed and they are called the molar reaction enthalpy and the molar reaction entropy.

By this computational approach, the reaction equation simplifies to a reaction which leads from the "mean value E" (educt) with prototypically conceived median particles to a "mean value P" (product) with other, also prototypically imagined median particles. This view characterizes the actual thermodynamic quality of the investigated reaction better than the description "combustion enthalpy" of a substance arbitrarily selected from the reaction mixture.
Everyone knows that combustion reactions are exothermic. It was shown in section 7.1 that a reduction in thermal storage capacity can lead to a temperature increase. From the values given above it is seen that the reaction entropy indeed is negative, that is, the end substances have a smaller entropy than the starting substances. However, this difference appears to be too small to understand the strong exothermic combustion and the large temperature increase during combustion process. A second "set screw" for the course of the reaction temperature has already been mentioned in section 7.1: the energetic height of the lowest energy level.
The energetic height of the lowest energy level is related to the definition of the zero level. The state in which all the atoms of a substance are separated from one another to infinitely great distances is a suitable comparison state for all substances. If a real substance with real particle distances is constructed from this comparison state, a characteristic energy is obtained for the real substance. The energetic difference between the comparison state and the characteristic energy is the dissociation energy. In the case of reactions with several substances, always one of these substances has the greatest dissociation energy. The lowest energy level of this substance defines the zero level of this particular reaction, and the lowest levels of the other substances are then obtained from the different dissociation energies.
Before we focus on this second "set-screw" in section 7.4, however, we will first turn to real trials. In order to approach the complex issue of chemical equilibrium in a meaningful manner, we will deal with very simple processes of the type E <=> P in this chapter.

In two video sequences it is shown that the equilibrium is established both by the starting side and by the product side in spontaneous processes.
Look at the spontaneous endothermic formation of the products.

Video with Sound: Spontaneous Endothermic Path to Equilibrium, Forward Reaction

One can very impressively observe how the drive for the spontaneous formation of the equilibrium decreases from very large values to zero in about 90 seconds. The temperature drops by 3K.
The evidence that an equilibrium was reached after the drive decreased to zero is based on the principle of Le Chatelier. If the probe is removes with the adherent reactant from the calorimeter, product particles are removed from the equilibrium, ie the evaporated ethanol, which is still in the calorimeter space and not outside. Therefore, the starting side attempts to endothermically build further products
Now look at the spontaneous setting of the equilibrium from the product side.

Video with Sound: Spontaneous Exothermic Path to Equilibrium, Back Reaction