Bringt man zwei (oder mehr) Stoffe in thermischen Kontakt, so beobachten wir, dass spontan ein bestimmter Prozess einsetzt, der "automatisch" zu einem bestimmten Endzustand führt. Dieser Zustand ist stets dadurch gekennzeichnet, dass alle beteiligten Stoffe die gleiche Temperatur annehmen. Für den täglichen Umgang ist es von Interesse, zu verstehen, wodurch bestimmt wird, wo diese Endtemperatur liegt - näher bei der Temperatur des heißesten oder des kältesten Stoffs.

Um die Verhältnisse einfach zu halten, beschränken wir uns im folgenden Versuch auf nur zwei Stoffe für den thermischen Kontakt. Wir bringen ein Metall in siedendem Wasser zunächst auf die Temperatur von ca. 100 °C und bereiten in der Zwischenzeit ein Thermosgefäß (Kalorimeter) so vor, dass sich darin kaltes Wasser (Raumtemperatur) und eine Temperatur-Messsonde befinden. Im Metallkörper steckt ebenfalls eine Temperaturmesssonde, so dass man die Entwicklung beider Temperaturen beobachten kann, wenn wir das heiße Metall ins kalte Wasser eintauchen.

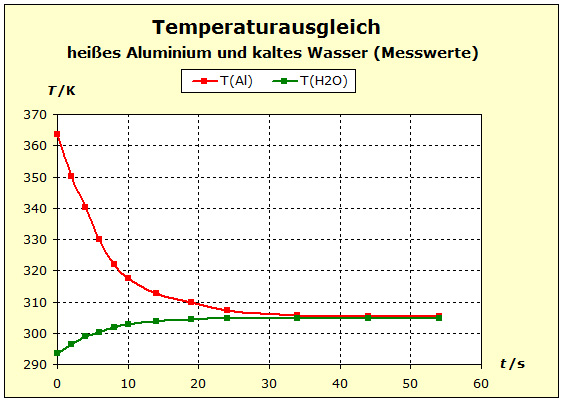
Video: Temperaturausgleich zwischen heißem Aluminium und kaltem Wasser

Das heiße Aluminium hat sehr viel von seiner anfänglichen Temperatur verloren, während sich das kalte Wasser kaum erwärmt hat. Wasser ist offensichtlich ein thermisch träger Stoff, er ändert seine Temperatur nur geringfügig.

Wir wiederholen den vorigen Versuch aber nehmen diesmal als Metall einen heißen Kupferblock. Wir wollen sehen, ob das edlere Metall Kupfer in der Lage sein wird, seine thermische Energie besser bei sich zu behalten als das Aluminium. Das wäre dann der Fall, wenn die Endtemperatur im folgenden Experiment höher liegt als beim Temperaturausgleich zwischen Aluminium und Wasser.

Video: Temperaturausgleich zwischen heißem Kupfer und kaltem Wasser

Beim Entauchen in das kalte Wasser haben die beiden Metalle mit 91°C (364K) etwa die gleiche Ausgangstemperatur und das Wasser ist etwa 20°C (293K) "kalt". Man erkennt aber auch einen Unterschied in der thermischen Trägheit zwischen Aluminium und Kupfer: beim Aluminium wird die Temperatur um etwa 4 K weniger abgesenkt als beim Kupfer. Der Aluminiumblock verhält sich thermisch also träger als der Kupferblock. Die Temperatur des Wassers steigt beim Aluminium stärker als beim Kupfer: ΔT(Wasser,Al) ≈ 11 K; ΔT(Wasser,Cu) ≈ 7 K. Deshalb kann man schließen, dass der Aluminiumblock an der Wasserportion deutlich mehr (ca. 60%) thermische Arbeit verrichtet als der Kupferblock.

Nun gilt es jedoch zu bedenken, dass in 100g Aluminium etwa 3,7 mol Atome enthalten sind, während 100g Kupfer nur etwa aus 1,6 mol Atomen besteht. In unseren Experimenten ist die thermische Trägheit des Aluminiums durch die große Atomanzahl hervorgerufen. Vergleicht man nämlich die molaren Standardentropien* der beiden Stoffe, so findet man die Werte:

S/R(Al)= 3,41

S/R(Cu)= 3,99

Für die Thermokapazitäten findet man:

C_p/R(Al)= 2,93

C_p/R(Cu)= 2,94

Die Thermokapazität des Kupfer ist also nur sehr geringfügig größer als die des Aluminiums, so dass man auch nach diesem Befund feststellt, dass die thermische Trägheit des Aluminiums in obigem Experiment der großen Anzahl der Atome geschuldet ist. In den Abschnitten 3.3 und 3.4 wurden bereits Diagramme gezeigt, die systematisch für die Stoffe im Periodischen System der Elemente zeigen, dass die Thermokapazitäten sich zwar gleichartig, aber wesentlich geringer ändern als die molaren Standardentropien.

* Da die Metalle nicht aus Molekülen bestehen haben die molaren Entropien dieselben Zahlenwerte wie die atomaren Entropien.

Auf der Modellebene lassen sich die in den vorigen Experimenten gezeigten Phänomene auf verschiedene Arten darstellen. In den beiden nächsten Videos wird das Fluidmodell mit Getränkeflaschen als Modellversuch eingesetzt und dabei der Temperaturausgleich zwischen Aluminium und Wasser, bzw. Kupfer und Wasser nachvollzogen. Es kommt in beiden Fällen zu einer Endtemperatur, die näher bei der Anfangstemperatur des Stoffes mit der größeren Standardentropie liegt.
Da im Fluidmodell die Querschnittsfläche der Standardentropie entspricht, wurde als Modell für das Wasser die Flasche mit dem größten Querschnitt eingesetzt. Die Flasche mit dem kleinsten Querschnitt entspricht dem Kupferblock.

Video: Modellversuch zum Temperaturausgleich zwischen Aluminium und Wasser

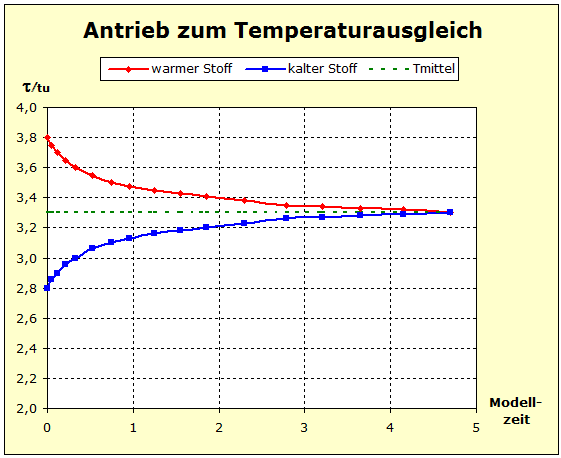
Video: Modellversuch zum Temperaturausgleich zwischen Kupfer und Wasser

Man erkennt aus dem Diagramm sehr gut, dass die thermische Trägheit beim Wasser am größten ist und dass das Aluminium in der thermischen Trägheit aber das Kupfer übertrifft, weil die Temperatur des Aluminiums nicht so stark abgesenkt wird wie die des Kupfers.
Als Hilfslinie wurde die mittlere Temperatur eingezeichnet. Diese Endtemperatur wird nur erreicht, wenn die Standardentropien beider Stoffe gleich sind.

Das Fluidmodell erlaubt auch eine starke Vereinfachung, indem auf eine räumliche Darstellung des zylindrischen Speichergefäßes verzichtet wird. Dennoch erkennt man die wesentlichen Eigenschaften der dargestellten Stoffe, wie Entropie/Querschnitt und Temperatur/Füllhöhe. Der folgende Link verdeutlicht dies.

PDF: Temperaturausgleich zweier Stoffe mit unterschiedlicher Standardentropie
(vereinfachtes Fluidmodell)

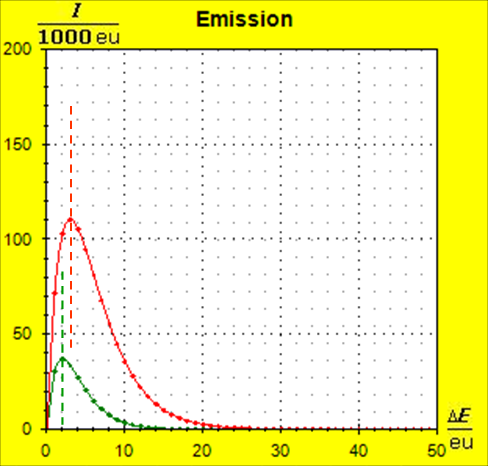
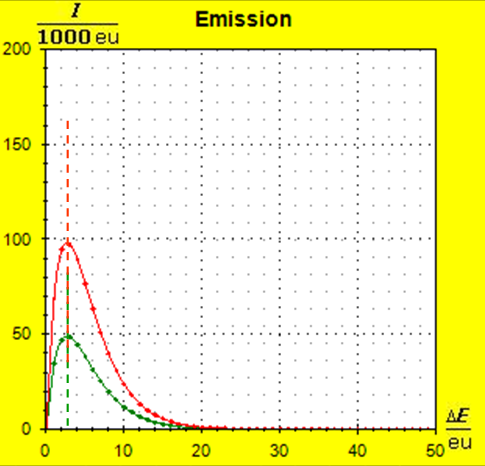
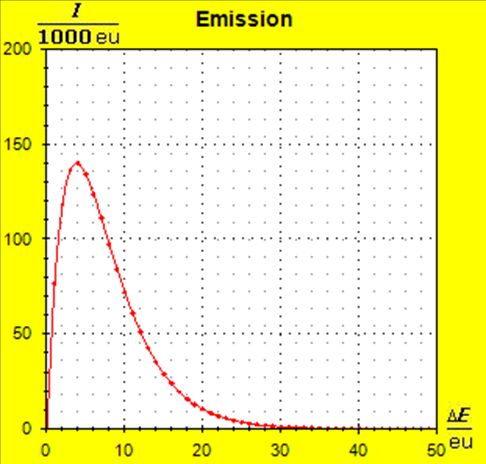
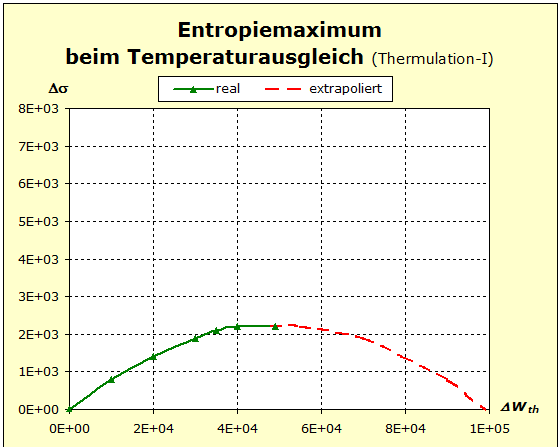
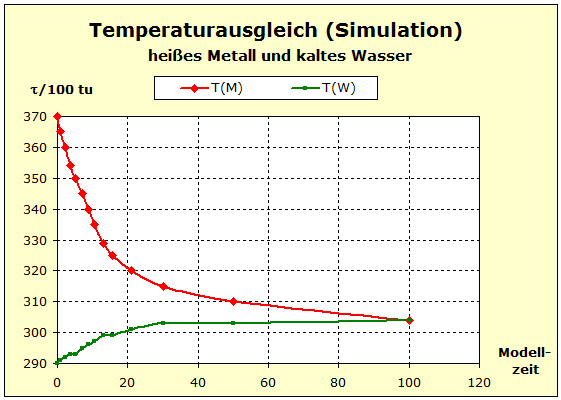
Möchte man jedoch die Zusammenhänge möglichst umfassend beschreiben, so wird man auf die quantentheoretischen Grundlagen zurückgreifen müssen. Dies ist mit dem Programm Thermulation-I auch leicht zu verwirklichen. Die folgende Animation zeigt einen Temperaturausgleich zwischen zwei verschiedenen Stoffen wie z. B. Metall und Wasser, wobei auch unterschiedliche Atomanzahlen und die quantentheoretischen Hintergründe dieses Prozesses berücksichtigt werden können. Die Simulation bildet den Vorgang des Temperaturausgleichs zwischen Kupfer und Wasser ab, so wie er im obigen Realexperiment durchgeführt wurde.

Wir gehen dabei in sechs Schritten vor:

1. Ermitteln der Standardwerte der atomaren Entropien von Aluminium und Wasser

2. Übertragen dieser Realwerte auf die Modellebene des Thermulation I Programms

3. Anpassen der Real- und Modellwerte an die beiden Ausgangstemperaturen von Aluminium und Wasser

4. Berücksichtigung der unterschiedlichen Atomanzahlen von 100g Aluminium und 100g Wasser

5. Animierte Darstellung der Simulation

6. Würdigung des Ergebnisses

Schritt 1:
Den Tabellenwerken entimmt man, dass unter Standardbedingungen die molare Entropie von Aluminium 28,33 J/(Kmol) beträgt. Da beim Aluminium 1 Mol des Stoffs aus 1 Mol Atomen besteht, ist dies bereits der gesuchte Wert der atomaren Standardentropie S_at(Al).
Anders beim Wasser. Den Tabellen entnimmt man den Wert der molaren Standardentropie von 69,91 J/(Kmol). Da 1 Mol Wasser aus 3 Mol Atomen besteht, muss man diesen Wert durch drei teilen. Also erhält man für das Wasser den atomaren Standardwert von S_at(H₂O)= 23,30 J/(Kmol). Dass dieser Wert kleiner ist als der von Aluminium benötigt eine Erläuterung, da Aluminum ein Feststoff, Wasser aber eine Flüssigkeit ist. Wir wissen aber, dass die durchschnittliche Atommasse im Aluminium 26,98 g/mol, im Wasser jedoch nur 18/3 g/mol = 6 g/mol beträgt. 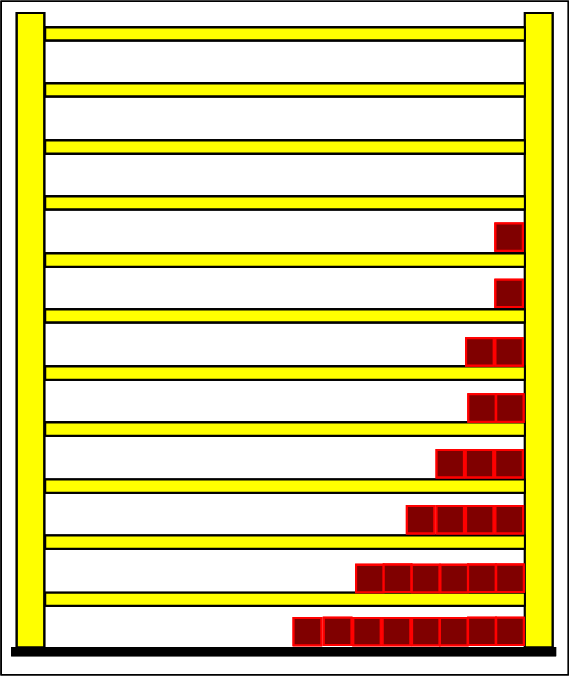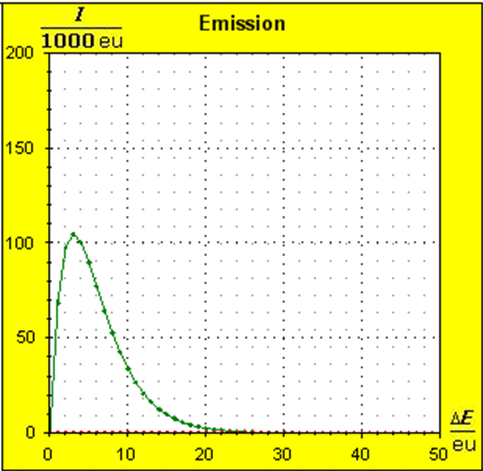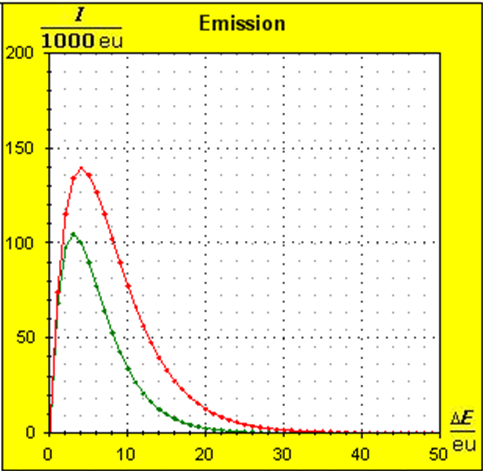Die kleine atomare Durchschnittsmasse macht den geringen Entropiewert des Wassers im Vergleich zum Aluminium verständlich.

Schritt 2:
Die beiden Entropiewerte stehen im Verhältnis:

S_at(Al):S_at(H₂O)= 28,33:23,30=1,22:1.

Auf der Modellebene müssen wir jetzt für Wasser und Aluminium zwei Energieniveauabstände suchen, die bei gleichen Atomanzahlen zu Entropiewerten führen, die an dieses Werteverhältnis gut angepasst sind. Die Werte ΔE(Al) = 1,7 eu und ΔE(H₂O) = 2,3 eu erfüllen diese Bedingung auf der Modellebene in Modelleinheiten gut und zwar für jeweils ca. 50000 Teilchen:

σ(A):σ(B)= 79000 : 64100 = 1,23 : 1

Diese Wahl ist zunächst willkürlich, denn man könnte sicherlich auch mit zwei anderen Niveauabständen ein angemessenes Entropieverhältnis auf der Modellebene finden. Wir wollen erreichen, dass die Werte im Boltzmann-Diagramm und beim Fluidmodell zu guten Visualisierungen führen. Deshalb wenden wir uns jetzt den weiteren Randbedingungen zu, die die realen Stoffe vorgeben und beurteilen dann am Ende, ob diese Wahl geschickt war.

Die beiden folgenden Bilder zeigen die Standardwerte der beiden modellierten Stoffe. Die beiden blauen Halbwertsenergielinien sind sichtbar gleich lang und die Temperaturskalen am Fluidzylinder zeigen die gleiche Füllhöhe an.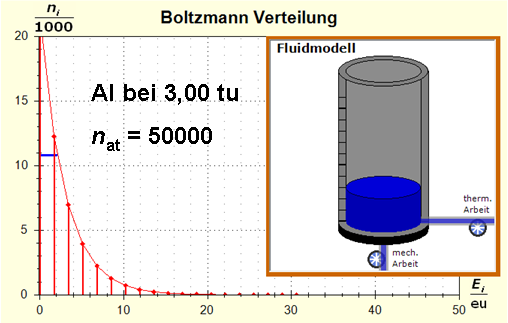

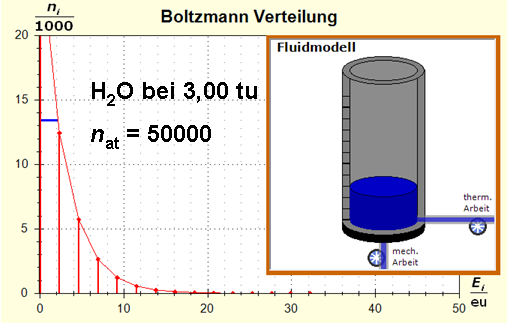Man erkennt gut, dass Aluminium wegen der 4,5 mal so großen mitteren Atommasse die enger liegenden Niveaus hat. Wegen des größeren Querschnitts des Fluidspeichers, würde man bisher die größere thermische Trägheit beim Aluminium erwarten.

Schritt 3: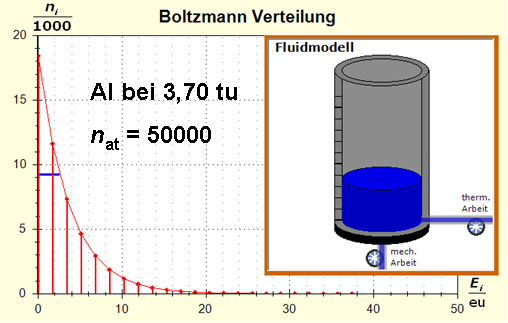
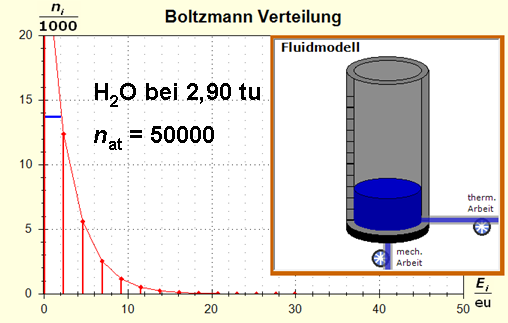Als nächstes müssen wir die beiden Modellstoffe auf ihre Ausgangstemperaturen bringen:
τ(Al) = 3,70 tu und τ(H₂O) = 2,90 tu.
Es wurde oben schon einmal darauf hingewiesen, dass wir auf der Modellebene gute Ergebnisse erzielen, wenn man die Kelvintemperaturen bei der Übertragung auf das Modell durch 100 teilt. Die Ausgangstemperatur für den Aluminiumblock war die Siedetemperatur des Wassers, also etwa 370 K und das kalte Wasser hatte eine Temperatur von 290 K (ca. 20°C). Die Modellbilder sehen so aus:

Wegen der größeren Temperatur im Aluminium (erkennbar an der längeren blauen Halbwertsenergielinie und der größeren Füllhöhe) hat der Querschnitt, also die Entropie im Fluidmodell nochmal zugenommen und die thermische Trägheit vergrößert. Im Wasser erscheint die thermische Trägheit durch Absenkung der Temperatur noch etwas abgenommen zu haben.

Schritt 4:
In diesem Schritt müssen wir uns über das Atomanzahlverhältnis der beiden Portionen 100g Al und 100g H₂O klar werden. Dazu teilen wir die Masse 100g durch die Durchschnittsmassen:

Al :    100g : 26,98 g/mol = 3,71 mol = 3,71 ^. 6e+23 Atome = 2,22e+24

H₂O :    100g : 6,00 g/mol = 16,7 mol = 16,7 ^. 6e+23 Atome = 1,00e+25

Diese Werte übertragen wir in ihrer Relation auf die Modellebene, indem wir für Wasser die im Programm vorgesehene Anzahl von 50000 und für Aluminium 11100 Atome wählen. Jetzt endlich erhalten wir die tatsächliche Ausgangssituatiuon für unser Modellexperiment: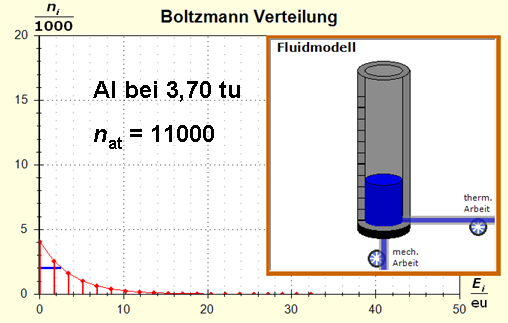

Jetzt hat sich das Bild entscheidend geändert: Durch die kleine Stoffportion des Aluminiums ist die Entropie und damit die thermische Trägheit dieser Metallportion deutlich gesunken.

Schritt 5:
Bevor uns jetzt dann der eigentlichen Simulation zuwenden, müssen wir noch bedenken, dass wir das Experiment so durchgeführt haben, dass beide Stoffe in einem isolierten System zwar miteinander aber nicht mit der Umgebung Energie austauschen konnten. In der animierten Darstellung fehlen deshalb die Wege, über die mechanische oder thermische Arbeit an der Umgebung oder umgekehrt am System aus den beiden Stoffen verrichtet werden kann.

Animation: Temperaturausgleich zwischen Aluminium und Wasser

Schritt 6:
Für die zeitliche Darstellung der Simulation im folgenden Diagramm wurde angenommen, dass für gleiche thermische Arbeitsbeträge im Verlauf des Experiments zunehmend längere Zeitspannen benötigt werden. Die gleichen thermischen Arbeitsbeträge bestehen darin, dass die Photonen gleich große thermische Energiebeträge vom heißen auf den kälteren Stoff übertragen.

Die beiden Schaubilder zeigen eindrucksvoll, dass die sorgfältige Ermittlung der quantentheoretischen Grundlagen dieser Simulation zu einer angemessenen Darstellung des Realexperiments geführt haben. Für die Entropie und ihre Bedeutung für die thermische Trägheit eines Stoffes muss man offensichtlich außer den Rückstellkräften, den Teilchenmassen auch die Teilchanzahlen als Einflussfaktoren im Auge behalten.
Mit dem Thermulation-I Programm gelingt auch für das Kupfer-Wasser Experiment eine gleich gute Simulation, wenn man die quantentheoretischen Grundlagen entsprechend sorgfältig wie beim Aluminium einrichtet.

Beobachtet man natürliche Prozesse, die spontan und freiwillig ablaufen, so ergeben sich vier grundsätzliche Fragen, die für die Deutung des Antriebsphänomens entscheidend sind. Wie kann man verstehen, dass

1. der Vorgang spontan startet?
2. die Prozessgeschwindigkeit im Verlauf des Vorgangs abnimmt?
3. eventuell der Vorgang auf "halber Strecke zum Stillstand" kommt?
4. es eventuell auch für einen Umkehrvorgang einen Antrieb geben kann?

In diesem Abschnitt wollen wir uns einem Versuch zuwenden, der für das Verständnis des thermodynamischen Antriebs grundlegend ist. Obwohl die Idee dieses Experiments sehr einfach ist, so bestehen gleichwohl viele Schwierigkeiten, die Durchführung so zu gestalten, dass der tatsächliche experimentelle Befund uns auf dem Weg zum Antrieb weiterhilft. Die einfache Idee des Versuchs heißt:
Wir bringen zwei gleich große Stoffportionen desselben Stoff aber mit unterschiedlichen Temperaturen in thermischen Kontakt miteinander und beobachten messend den Temperaturausgleich.

Auf den ersten Blick wird man dabei das Ergebnis erwarten, dass die Endtemperatur sich beim arithmetischen Mittel der beiden Ausgangstemperaturen einstellt. Das ist aber nur dann richtig, wenn man außer Acht lässt, dass man je nach Versuchsdurchführung mehr weniger gravierende systematische Fehler macht. Deshalb wollen wir in Vorüberlegungen die Versuchsbedingungen diskutieren.

1. Der Versuch soll mit jeweils 50 mL heißem und kaltem Wasser durchgeführt werden.
2. Wir lassen den Temperaturausgleich in einem Kalorimeter ablaufen.
3. Das Kalorimeter soll eine Zwischenwand haben. (s. Bild)

zu 1. : Es bietet sich an, für das Experiment einen flüssigen Stoff zu wählen, weil man gleich große Stoffportionen sehr einfach bestimmen kann. Wasser ist zudem leicht zugänglich. Allerdings muss man im Auge behalten, dass gleiche Volumina bei unterschiedlichen Temperaturen nicht gleich viele Atome enthalten. Da das kalte Wasser bei Raumtemperatur vorliegt, wird die Dichteanomalie den Ablauf nicht wesentlich beeinflussen. Zwischen zwei festen Stoffen wäre der thermische Kontakt schwieriger herzustellen, wenn es sich z. B. um Metallblöcke oder größere Kristalle (Kandiszucker o. ä.) handeln würde. Metallpulver oder pulverisierte Kristalle wären durchaus eine Alternative.
zu 2.: Damit sich der Temperaturausgleich auf die beiden gewählten Stoffportionen beschränkt und möglichst wenig thermische Energie auf die Umgebung übertragen wird, lassen wir das Experiment in einem Kalorimeter ablaufen. Allerdings müssen wir dabei beachten, dass auch das beste Kalorimeter kein perfekt isoliertes System darstellt und sich natürlich auch Kalorimeterbauteile in thermischem Kontakt mit den beiden Ausgangsstoffen befinden.
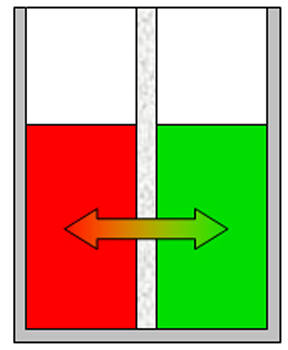
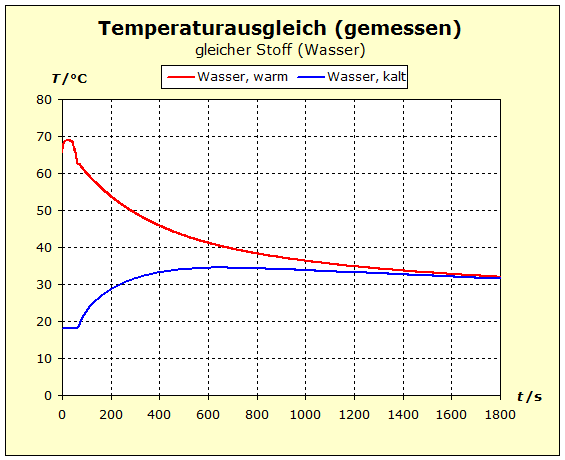
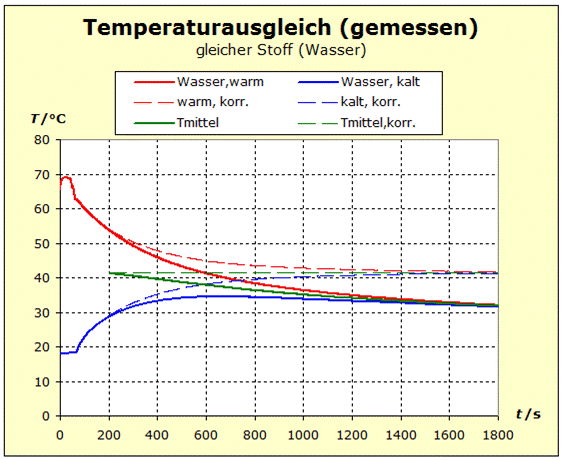
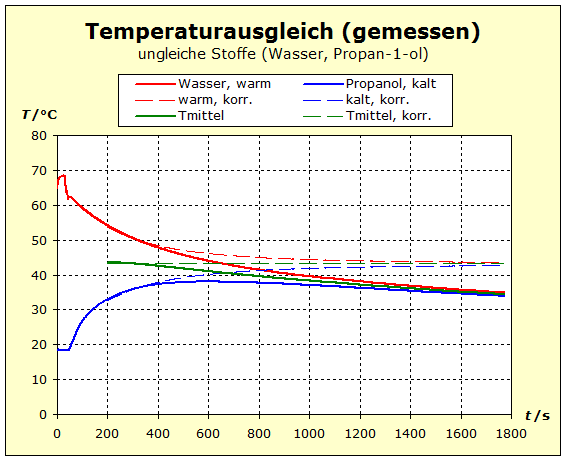
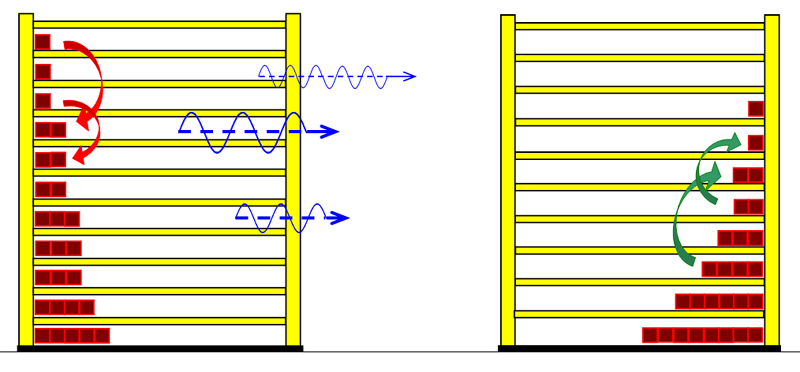
zu 3. : Wir wollen die beiden Wasserportionen nicht durch Umrühren miteinander vermischen und verwenden deshalb ein Kalorimeter mit einer Zwischenwand, so wie man es in thermdynamischem Kontext häufig auch in Lehrbüchern findet. Der quantentheoretische Hintergrund ist der Folgende: Energie wird von den hochliegenden Energieniveaus des heißeren Stoffs auf die niedrigeren Energieniveaus des kalten Stoff übertragen. Es ändern sich also in beiden Stoffportionen die Anzahl der besetzten Niveaus und damit die Entropie. Um eine Diskussion zu vermeiden über das, was die klassische Thermodynamik als Mischungsentropie bezeichnet, sollen hier die Wasserportionen nicht vermischt werden. Der thermische Kontakt wird über eine dünne Kunststofftrennwand hergestellt. Dadurch ergibt sich eine niedrige Prozessgeschwindigkeit. Bei zwei gleichen Stoffen würde wohl auch klassisch keine Mischungsentropie auftreten, wenn wir hier trotzdem die Mischungsfrage ausklammern, so können wir denselben Versuchsaufbau auch für andere Stoffkombinationen verwenden. Zum quantentheoretische Hintergrund gehört auch ein weiterer Aspekt: Die Entropie setzt sich aus verschiedenen Anteilen zusammen und wird über die Verteilungsfunktionen (partition function, Zustandssumme) der Translation, Rotation, Vibration und der Elektronenzustände ermittelt. Eine 'partition function of mixture' ist jedoch in der Literatur nicht beschrieben.
Ein weiterer Grund für die Verwendung eines geteilten Kalorimeters liegt darin, dass man natürlich auch an der Variation dieses Experiments mit zwei verschiedenen Stoffen, wie z. B. Alkohol und Wasser, interessiert ist. Dabei muss man natürlich ausschließen, dass die verschiedenen Stoffe mteinander reagieren. So ist es bekannt, dass Alkohol und Wasser exotherm miteinander reagieren.

Nach diesen Vorüberlegungen können Sie sich das Video zum Versuch anschauen. Da die Prozessgeschwindigkeit niedrig ist, dauert der Versuch real ca. 30 Minuten. Durch Zeitraffertechnik wurde das Video auf ca. 2 Minuten gestrafft.

Video mit Ton: Temperaturausgleich zwischen zwei Wasserportionen.

Die beiden folgenden Diagramme zeigen die Messdaten. Trotz praktisch gleicher Ausgangstemperaturen verlaufen die Temperaturkurven deutlich unterschiedlich: Im Falle des Stoffpaares Wasser/Propan-1-ol liegen sowohl die obere wie auch die untere Kurve jeweils höher als die entsprechende Kurve des Stoffpaares Wasser/Wasser. In beiden Fällen stellt sich keine eindeutige Endtemperatur ein, sondern es wird während der Versuchsdauer thermische Energie abgestrahlt.
Die höchste Temperatur, die das kalte Wasser erreicht, liegt bei 34,5 °C, während der kalte Alkohohl sich bis auf 38°C erwärmt. Der Alkohol ist offenbar thermisch weniger träge als das Wasser.

In die beiden folgenden Diagramme wurde eine dritte Kurve eingezeichnet, die die arithmetischen Mittelwerte der oberen und der unteren Temperaturkurven anzeigt. Die mittlere Temperatur sinkt in beiden Versuchen praktisch gleich stark um 9,5 bzw. um 9,2 K.

Da die Abkühlung der Apparatur so ermittelt wurde, lässt sich der Abkühlungseffekt aus den Messdaten näherungsweise herausrechnen. Dies zeigt das folgende linke Diagramm.
Schwieriger ist es die thermische Trägheit des Kalorimeters zu erfassen, weil einerseits beim Umfüllen das heißen Wassers thermische Energie abgestrahlt wird, und andererseits die thermische Energie des Wassers zunächst die Apparatur erwärmt, bevor diese Energie in die Umgebung abfließt. Im arithmetischen Mittelwert der Ausgangstemperaturen (43,5°C) liegt jedoch sicherlich eine obere Grenze, bis zu der die zuerwartende Endtemperatur für ein ideal isoliertes und trägheitsloses Kalorimeter angenommen werden kann.

Mit dieser Auswertung liegen wir sehr nah an einem zu erwartendem Befund in einem als ideal angenommenen Kalorimeter. Von dieser Annahme ausgehend wollen wir den thermodynamischen Antrieb zu diesem Prozess weiter herausarbeiten.

Das linke Bild zeigt eine Boltzmann-Verteilung für einen Stoff mit hoher Temperatur.
Da die Besetzungszahlen nur langsam abnehmen, ist die Halb- wertsenergie hoch. Das rechte Bild zeigt ein modellhaft zugehöriges Emissionsspektrum. Auf der senk- rechten Achse ist die Emissions- intensität als Anzahl der emittierten Photonen pro Zeiteinheit aufge- tragen.

Diese beiden Darstellungen ver- gleichen wir nun mit den ent- sprechenden Bildern für einen Stoff mit niedriger Temperatur.

Das linke Bild zeigt eine Boltzmann-Verteilung für einen Stoff mit gleicher Teilchenanzahl wie im vorigen Beispiel aber bei niedriger Temperatur.
Da die Besetzungszahlen hier rasch abnehmen, ist die Halbwertsenergie gering. Ein modellhaft zugehöriges Emissionspektrum zeigt das rechte Bild.

Vergleicht man die Spektren der beiden Beispiele, so erkennt man, dass der wärmere Stoff die höhere Strahlungsintensität erbringt und dass das Maximum seines Spektrums bei einem höheren Energiewert liegt.

Beide Stoffe emittieren spontan entsprechend ihrer Temperatur. Das rechte Bild zeigt beide Spektren in einem Schaubild. Man erkennt, dass der heißere Stoffes trotz gleicher Teilchenanzahl deutlich mehr thermische Energie durch Emission abgibt als der kalte Stoff.
Wenn beide Stoffportionen in einem nach außen hin isoliertem System vorliegen, können sich beide nicht gegen die Absorption der Strahlung wehren, die sich in diesem System befindet. Das führt dazu, dass der wärmere Stoff auch Photonen des kälteren aufnimmt. Bilanziert man aber die Strahlungsanteile, so verrichtet der wärmere Stoff netto thermische Arbeit am kälteren. Die Temperatur des kältern steigt, des wärmeren sinkt. Entsprechend verhalten die Emissionsspektren: Die Emission des wärmeren wird geringer, die des kälteren wird stärker. Die beiden Strahlungsmaxima nähern sich einander an. Solange einer Stoffe mehr Strahlung emittiert als der andere, besteht ein Antrieb für den spontanen Temperaturausgleich.
Dieser thermodynamische Antrieb liegt in der spontanen Emission begründet.

Das obige Bild fasst diese Situation zusammen. Der wärmere Stoff wird durch das linke Regal beschrieben, der kältere durch das rechte Regal. Der blau gezeichnete Photonenstrom stellt nur den Nettoanteil der thermischen Strahlung dar, die vom wärmeren mehr emittiert wird als vom kälteren Stoff. Beide Stoffe sind der insgesamt von beiden emittierten Strahlung ausgesetzt. Dadurch ist der kältere Stoff einer größeren Intensität ausgesetzt als er selbst emittiert: seine Temperatur steigt. Beim wärmeren Stoff ist es gerade umgekehrt. Nur der Nettoanteil der Strahlung des wärmeren verrichtet die thermische Arbeit am kälteren, die zur Temperaturerhöhung des kälteren und zur Temperatursenkung des wärmeren Stoffes führt.
Da die Intensitätsunterschiede der Emissionen der beiden Stoffe im Verlauf des Prozesses geringer werden, nimmt auch der thermodynamische Antrieb mit der Zeit ab.
Einen zeitlichen Verlauf dieses gesamten Prozesses auf der Ebene der Emissionsspektren zeigt die folgende Animation.

Animation: Temperaturausgleich zwischen zwei Stoffportionen.

Den zeitlichen Verlauf dieser Animation zeigt auch das folgende Schaubild. Man vergleiche dieses Schaubild mit den aus den Messwerten erstellten Diagrammen, die am Anfang dieses Abschnitts (6.2.2.) abgebildet waren.

Zwei weitere Fälle dieses Temperaturausgleichs sollen noch diskutiert werden:
1. Ungleiche Portionen desselben Stoffs
2. ungleiche Portionen von zwei verschiedenen Stoffen.

1. Bei ungleichen Portionen desselben Stoffs mit unterschieldichen Temperaturen wird man auch in einem ideal isolierten System erwarten, dass die Endtemperatur nicht mehr genau in der Mitte liegt. Die Emissionsspektren von Ausgangs- und Endsituation zeigen die beiden folgenden Bilder.

2. Bei verschiedenen Stoffen mit unterschiedlichen Temperaturen muss man sich den Unterschied in den Emissionskurven noch einmal verdeutlichen. Betrachten Sie die beiden folgenden Bilder. Sie zeigen zwei verschiedene Stoffe bei gleicher Temperatur und Teilchenanzahl:

Dass beide Stoffe trotz unterschiedlicher Niveaudichte über das ganze Spektrum hin gleich viele Photonen mit jeweils gleichen Frequenzen ausstrahlen, liegt daran, dass die Besetzungszahlen der Niveaus unterschiedlich sind. Bei geringem Niveauabstand sind die Besetzungszahlen geringer, aber es sind mehr Niveaus besetzt. Dadurch erfolgen gleich viele gleichfrequente Übergänge aber ausgehend von einer größeren Zahl von Niveaus.
Insgesamt wird man auch hier erwarten, dass das thermische Gleichgewicht dann erreicht ist, wenn aus jedem Teilvolumen die Strahlungsleistung gleich ist.

Es sei noch darauf hin- gewiesen, dass die Entro- pie bis zum Tempera- turausgleich ansteigt. Das Simulationsprogramm er- gibt die Entropiezunahme des nebenstehenden Dia- gramms.
Dass es sich tatsächlich um ein relatives Maximum handelt, lässt sich allerdings nur mit dem Programm simulieren, weil man dort auch nach Erreichen des thermischen Gleichgewichts immer noch weitere thermische Arbeit am zunächst kälteren, inzwischen aber heißeren Stoff verrichten kann. Im Realversuch ist dieser extrapolierte Zweig der Kurve so nicht erreichbar.