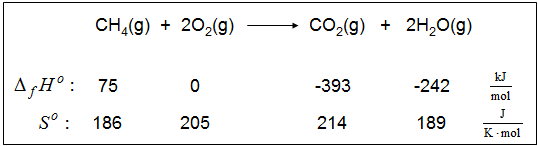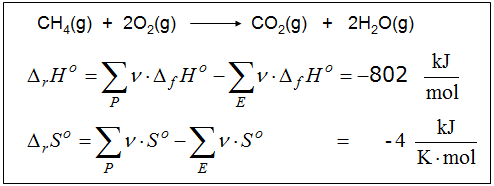In Publikationen und den thermodynamischen Tabellenwerken findet man nicht nur die Standardwerte von Enthalpie und Entropie der Bildungsreaktionen, sondern auch solche Werte über die Reaktionsenthalpien spezieller Reaktionen, wie z. B. Verbrennungsreaktionen. Dabei werden Reaktionsenthalpien dieses Reaktionstyps als Verbrennungsenthalpien oder Heizwerte analog zu den Bildungsenthalpien auf einzelne Stoffe bezogen. Als Beispiel sei hier einmal die Reaktionsgleichung für die Verbrennung von Erdgas angeführt:

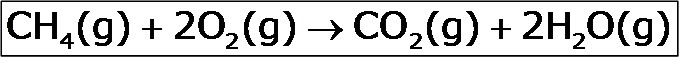
Wenn man solche Werte dann zur Beurteilung eines Stoffes wie Erdgas als Primärenergieträger heranzieht, so wirft dieses Vorgehen Fragen auf: Ist der Stoff Erdags ein Energieträger? Wer trägt welche Energie? Welche energetische Rolle spielen bei der Verbrennung der Sauerstoff und/oder die entstehenden Produkte?
Wir wollen zur Beantwortung dieser Fragen einmal die nächsten Schritte verfolgen und kommentieren, die in der klassischen Thermodynamik unternommen werden, um zu den Verbrennunsgenthalpien zu kommen.
1. Schritt:
Unter die Reaktionsgleichung schreibt man die Werte der molaren Standardbildungsenthalpien und der molaren Standardentropien.

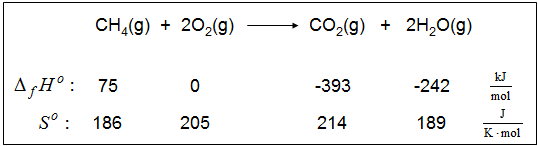
2. Schritt:
Man bildet auf beiden Seiten die Summen dieser Werte, nachdem man sie mit den jeweiligen stöchiometrischen Zahlen ν gewichtet hat.

Dieser Schritt erfordert in Bezug auf die gestellten Fragen dringend einen Kommentar, denn in diesen Werten kommt einerseits der Einfluss aller beteiligten Stoffe zum Ausdruck, andererseits sieht man diesen Werten nicht mehr an, ob sie aus zwei oder mehr Stoffen gebildet wurden. Sie könnten auch nur einen einzigen Stoff repräsentieren. Die Werte auf der Eduktseite charakterisieren die thermischen Eigenschaften der Eduktseite und die auf der Produktseite entsprechend die der Produktseite. Veranschaulichend kann man sagen, die Werte Eduktseite stehen für einen fiktiven Mittelwertsstoff mit gedachten Mittelwertsteilchen und die Werte der Produktseite charakterisieren auf gleiche Art einen entstehenden fiktiven Endstoff. Diese Sichtweise erscheint auch deshalb als gerechtfertigt, weil alle Reaktionen, bei denen sich für die Edukt- und Produktseite sich jeweils dieselben Werte ergeben, sich thermdynamisch äquivalent verhalten.
3. Schritt:
Man bildet die Differenzen dieser Werte und bezeichnet sie als molare Reaktionsenthalpie und als molare Reaktionsentropie.

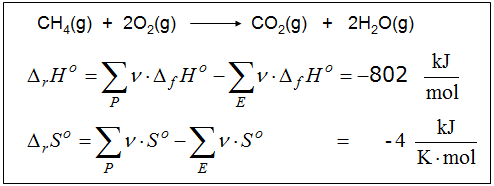
Durch dieses rechnerische Vorgehen vereinfacht sich die Reaktionsgleichung zu einer Reaktion, die vom "Mittelwertstoff E" mit prototypisch gedachten Mittelwertsteilchen zu einem "Mittelwertstoff P" mit anderen, ebenfalls prototypisch gedachten Mittelwertsteilchen führt. Diese Sichtweise charakterisiert die tatsächliche thermodynamische Qualität der untersuchten Reaktion besser, als es durch die Beschreibung "Verbrennungsenthalpie" eines willkürlich aus dem Reaktionsgemisch ausgewählten Stoffes geleistet wird.
Jeder weiß, dass die Verbrennunsgreaktionen exotherm verlaufen. In Abschnitt 7.1 wurde aufgezeigt, dass eine Verkleinerung der thermischen Speicherkapazität zu einer Temperaturerhöhung führen kann. Aus den oben angegebenen Werten ersieht man jedoch, dass die Reaktionsentropie zwar negativ ist, dass also die Endstoffe eine kleinere Entropie haben als die Ausgangsstoffe, aber die Differenz erscheint für die Exothermie der Verbrennung doch zu klein, als dass man damit die starken Temperaturanstiege beim Verbrennen plausibel machen kann. In Abschnitt 7.1 wurde bereits eine zweite "Stellschraube" für den Verlauf der Reaktionstemperatur erwähnt. Diese liegt in der Höhe des untersten Fachbodens im Speicherregal vor.
Die energetische Höhe des niedrigsten Energieniveaus steht in Zusammenhang mit der Definition des Nullniveaus. Der Zustand, in dem alle Atome einer Substanz auf unendlich große Entfernungen voneinander getrennt sind, ist für alle Substanzen ein geeigneter Vergleichszustand. Wird aus diesem Vergleichszustand eine reale Substanz mit realen Partikelabständen aufgebaut, so erhält man für die reale Substanz eine charakteristische Energie. Der energetische Unterschied zwischen dem Vergleichszustand und der charakteristischen Energie ist die Dissoziationsenergie. Bei Reaktionen mit mehreren Substanzen hat stets einer dieser Stoffe die größte Dissoziationsenergie. Das niedrigste Energieniveau dieser Substanz definiert das Nullniveau dieser besonderen Reaktion, und die niedrigsten Niveaus der anderen Substanzen werden dann aus den verschiedenen Dissoziationsenergien erhalten.
Bevor wir uns im Abschnitt 7.4. mit dieser zweiten "Stellschraube" beschäftigen werden, wollen wir uns aber zunächst wieder Realversuchen zuwenden. Um sich dem komplexen Thema des chemischen Gleichgewichts sinnvoll anzunähern, werden wir uns in diesem Kapitel zunächst mit sehr einfachen Prozessen des Typs E <=> P beschäftigen.

In zwei Videosequenzen wird gezeigt, dass sich das Gleichgewicht sowohl von der Eduktseite, wie von der Produktseite in spontanen Prozessen einstellt.
Betrachten Sie die spontane endotherme Hinreaktion.

Video mit Ton: Einstellung eines Gleichgewicht, Hinreaktion

Man kann sehr eindrucksvoll beobachten, wie der Antrieb für die spontane Gleichgewichtseinstellung von sehr großen Werten bis gegen Null innerhalb von etwa 90s abnimmt. Die Temperatur sinkt um 3K.
Der Nachweis, dass ein Geichgewicht erreicht wurde, nachdem der Antrieb versiegt war, basiert auf der Grundlage des Prinzips von Le Chatelier. Wenn man die Messsonde mit dem anhaftenden Edukt aus dem Kalorimeterraum herausnimmt, entzieht man dem Gleichgewicht Produktanteile, nämlich die verdunsteten Ethanoldämpfe, die nach wie vor im Kalorimeterraum sind. Deshalb versucht die Eduktseite diese endotherm nachzubilden.
Betrachten Sie nun auch die spontane Einstellung des Gleichgewichts von der Produktseite aus.

Video mit Ton: Einstellung eines Gleichgewichts, Rückreaktion