6.2. Thermal Equilibrium
|
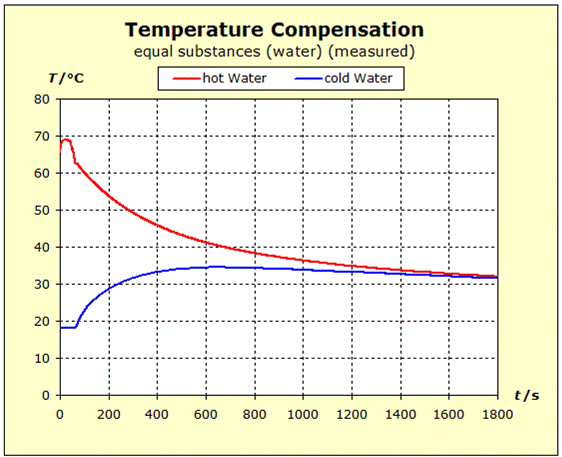
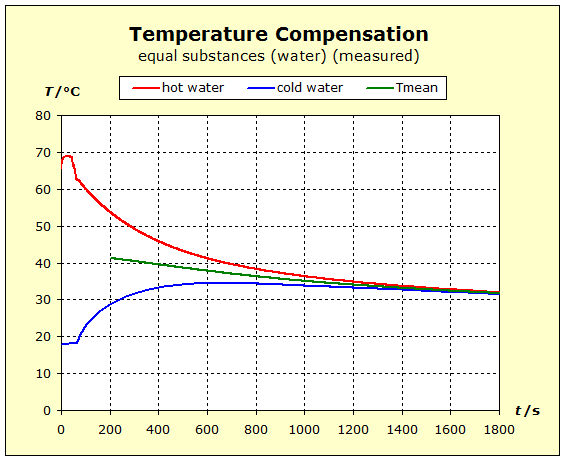
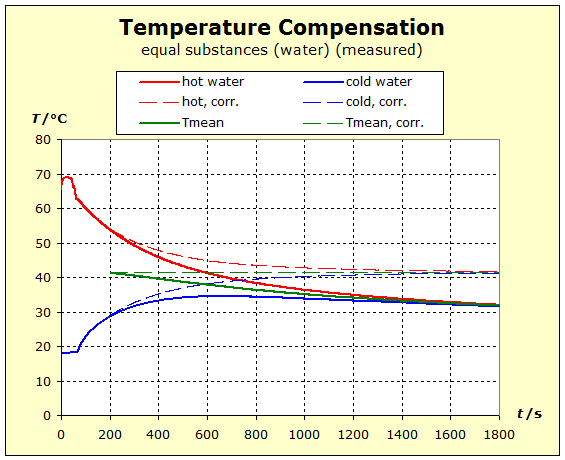
6.2.1. Temperature Compensation If two (or more) substances are brought into thermal contact, we observe that spontaneously a certain process, which "automatically" leads to a certain final state, spontaneously occurs. This condition is always characterized by the fact that all the substances involved assume the same temperature. For daily use, it is of interest to understand what determines the final temperature, closer to the temperature of the hottest or coldest substance. |
|
Video: Temperature Compensation Between Hot Aluminum and Cold Water The hot aluminum has lost very much of its initial temperature, while the cold water has barely warmed. Water is obviously a thermally inert substance, it only slightly changes its temperature. |
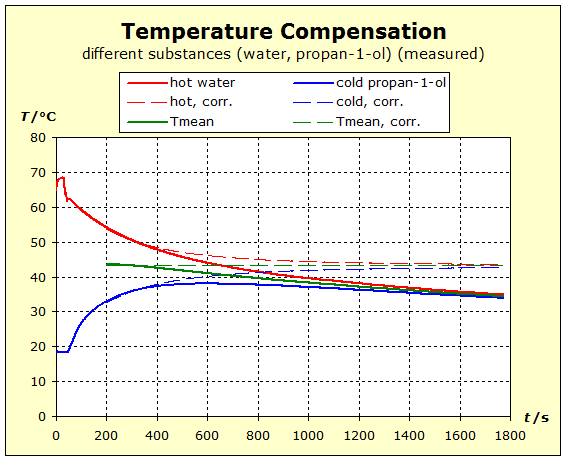
We repeat the previous experiment but this time take a hot copper block as a metal. We will see whether the nobler metal copper will be able to retain its thermal energy more readily than the aluminum. This would be the case if the final temperature is higher in the following experiment than in the temperature balance between aluminum and water.
Video: Temperature Compensation Between Hot Copper and Cold Water 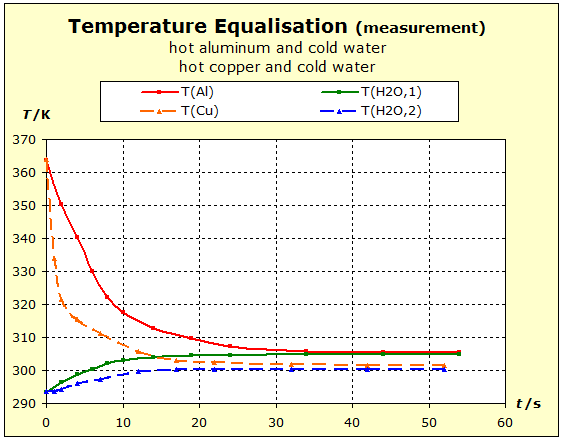 When immersed in the cold water, the two metals at 91°C (364K) have about the same starting temperature and the water is about 20°C (293K) "cold". The two experiments show that water is thermally more inert than metal blocks with the same mass as the water. However, there is also a difference in the thermal inertia between aluminum and copper: in the case of aluminum, the temperature is lowered by about 4 K less than in the case of copper. The aluminum block is thermally more inert than the copper block. The temperature of the water increases with the aluminum more than with the copper: ΔT(water, Al)= 11K; ΔT(water, Cu) = 7K. Therefore, it can be concluded that the aluminum block performs much more (about 57%; 11/7=1,57) thermal work on the water amount than the copper block.
S/R(Al)= 3,41 S/R(Cu)= 3,99 The thermal capacities are: Cp/R(Al)= 2,93 Cp/R(Cu)= 2,94 The thermal capacity of the copper is therefore only very slightly greater than that of the aluminum, so that it is also found from this finding that the thermal inertia of the aluminum in the above experiment is due to the large number of atoms. In sections 3.3 and 3.4, diagrams have already been shown which show systematically for the substances in the periodic system of the elements that the thermal capacities change in the same way, but substantially less, than the molar standard entropies. * Since the metals do not consist of molecules, the molar entropies have the same numbers as the atomic entropies. |
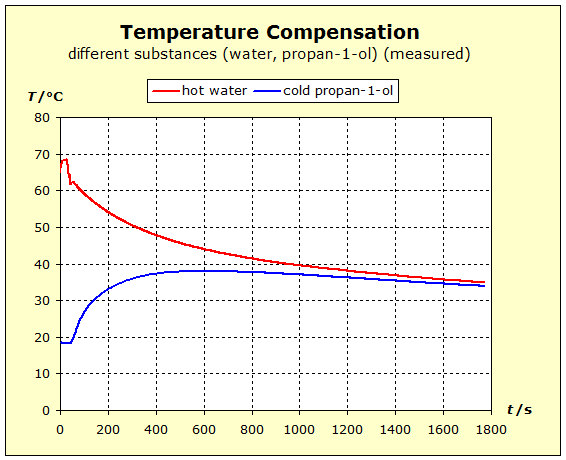
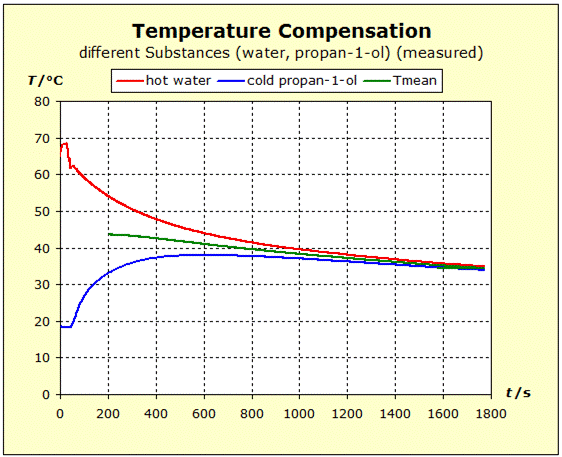
On the model plane the phenomena shown in the previous experiments can be represented in different ways. In the next two videos, the fluid model with beverage bottles is used as a model experiment and the temperature balance between aluminum and water, or copper and water, is reproduced. In both cases, the end temperature is closer to the initial temperature of the substance with the larger standard entropy. |
Video: Model Attempt to Temperature Compensation Between Aluminum and Water |
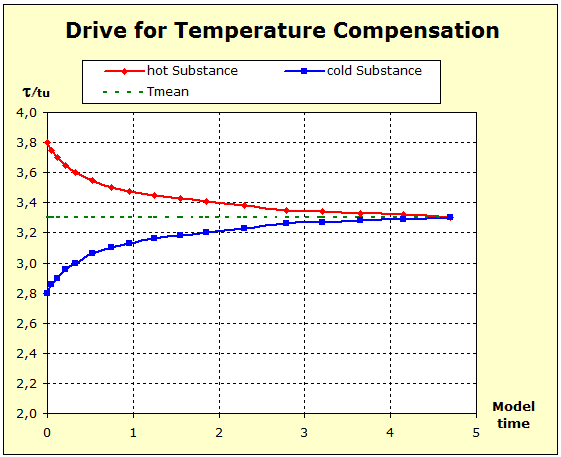
Video: Model Attempt to Temperature Compensation Between Copper and Water 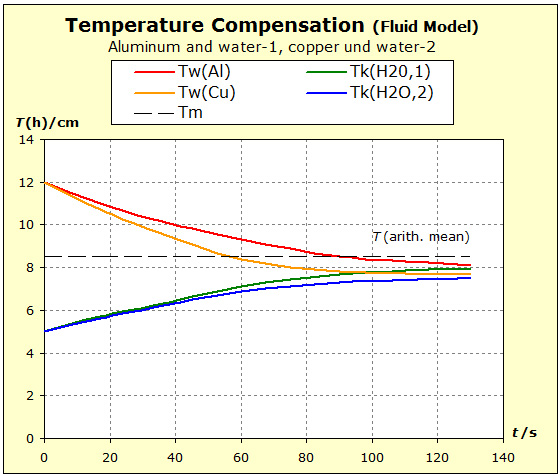 It can be seen from the diagram that the thermal inertia is the greatest in water, and that the aluminum in thermal inertia exceeds the copper because the temperature of the aluminum is not lowered as much as that of the copper The average temperature was plotted. This final temperature is reached only if the standard entropies of both substances are the same. |
The fluid model also permits a great simplification, since a spatial representation of the cylindrical storage vessel is dispensed with. Nevertheless, the essential properties of the substances shown, such as entropy / cross-section and temperature / filling height, can be seen. The following link illustrates this. |
PDF: Temperature Compensation of two Substances with Different Standard Entropy |
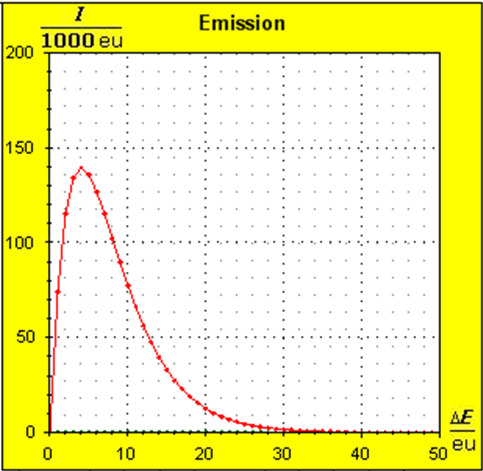
However, if one were to describe the context as comprehensively as possible, one would have to resort to the quantum theoretical bases. This is easy to achieve with the Thermulation-I program. The following animation shows a temperature balance between two different substances such as metal and water, whereby different atomic numbers and the quantum theoretical background of this process can be taken into account. The simulation depicts the process of temperature equilibrium between copper and water, as carried out in the above real-world experiment.
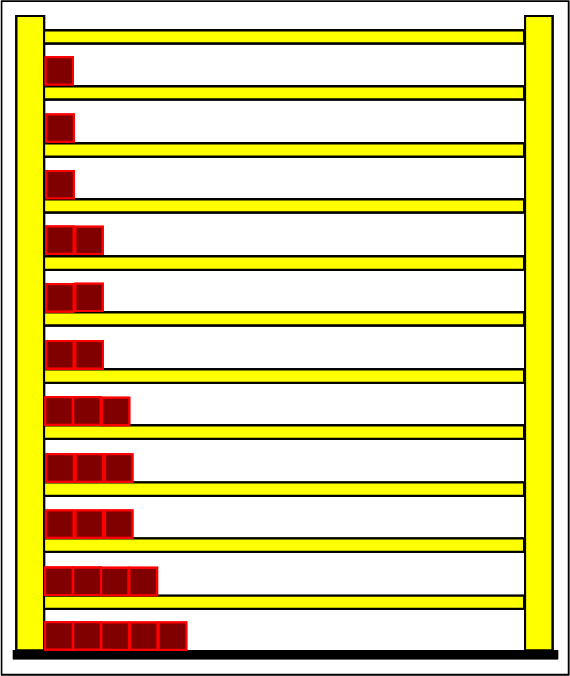
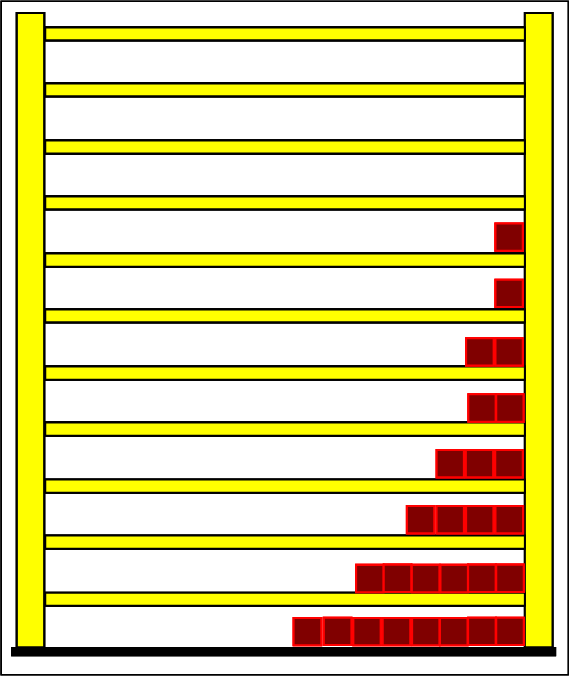
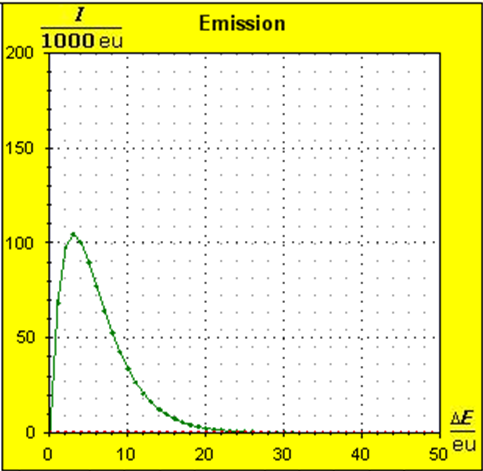
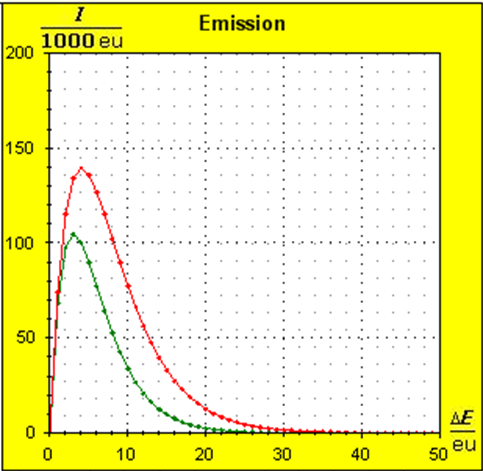
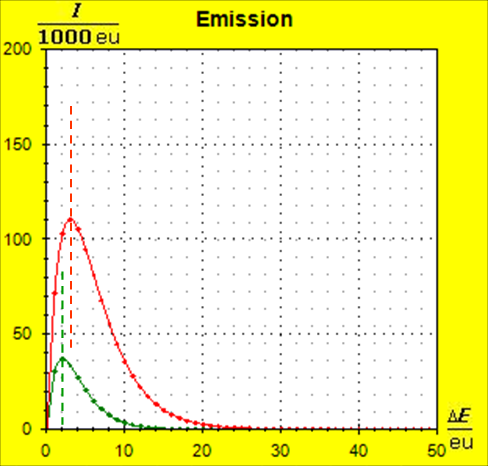
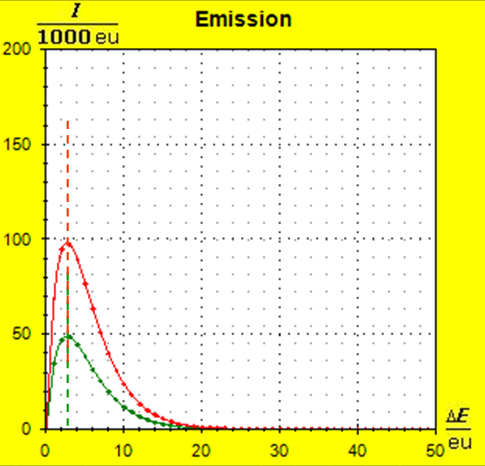
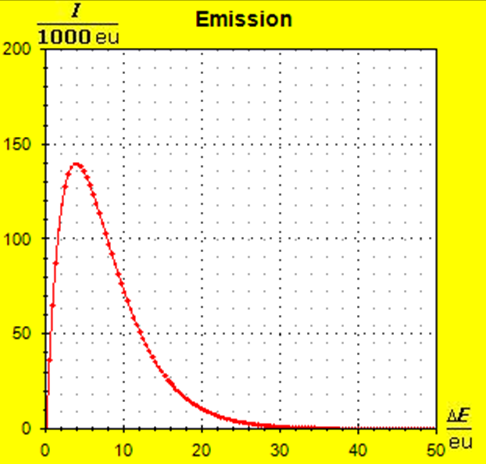
Step 1: Step 2: Sat(Al):Sat(H2O)= 28,33:23,30=1,22:1. On the model plane, we now have to look for two energy level distances for water and aluminum (equal number of atoms), which lead to such entropy values that adapt well to this ratio. The values ΔE(Al) = 1.7eu and ΔE(H2O) = 2.3eu fullfill the condition on the model plane in model units well and specifically for about 50000 particles each: σ(A):σ(B)= 79000 : 64100 = 1,23 : 1 This choice is at first arbitrary, because you could surely find an appropriate entropy ratio on the model plane with two different levels. The goal is to find values that lead to good visualizations in the Boltzmann diagram and the fluid model. Therefore, we now turn to the other constraints that the real substances pretend and then assess in the end whether this choice was neat. The two following pictures show the standard values of the two modeled substances. The two blue half-value energy lines are visibly equal in length and the temperature scales on the fluid cylinder show the same filling height. 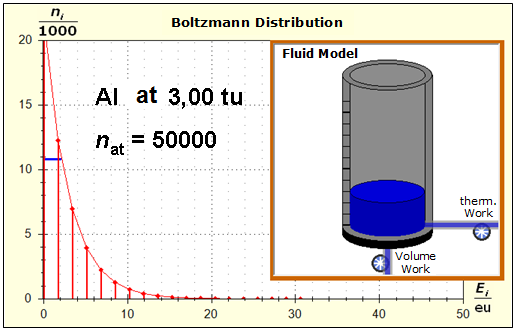
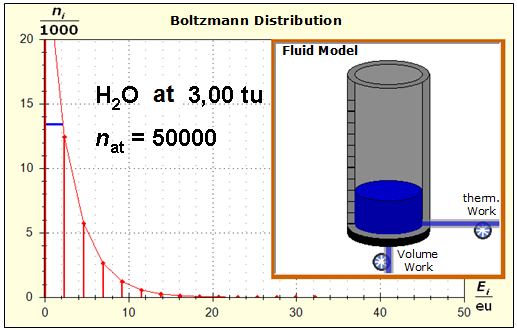 It is well to recognize that aluminum has the narrower energy level distances because of the 4.5 times as large atomic mass. Because of the larger cross-section of the fluid reservoir, the greater thermal inertia of the aluminum would be expected. Step 3: 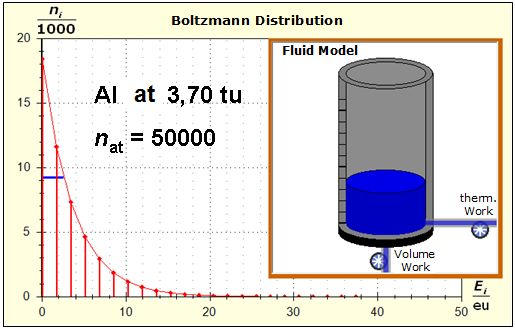
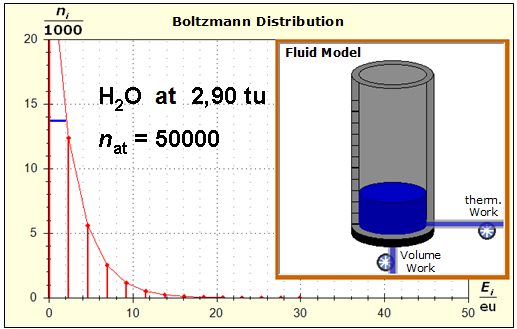 Because of the higher temperature in the aluminum (recognizable by the longer blue half-value energy line and the larger filling height), the cross-section, that is, the entropy in the fluid model, has once again increased and thermal inertia increased. In the water, the thermal inertia appears to have diminished somewhat by lowering the temperature. Step 4: Al : 100g : 26.98 g/mol = 3.71 mol = 3.71 . 6e+23 Atome = 2.22e+24 H2O : 100g : 6.00 g/mol = 16.7 mol = 16.7 . 6e+23 Atome = 1.00e+25 These values are transferred in their relation to the model plane by selecting for water the number of 50000 and 11100 atoms for aluminum. Now finally we get the actual starting situation for our model experiment: 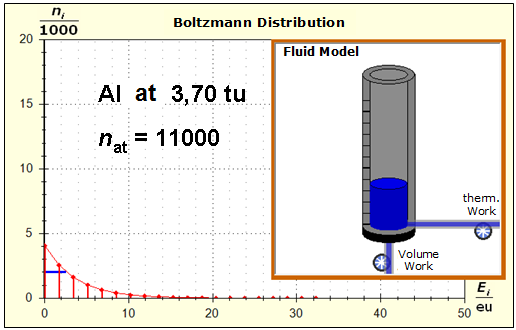
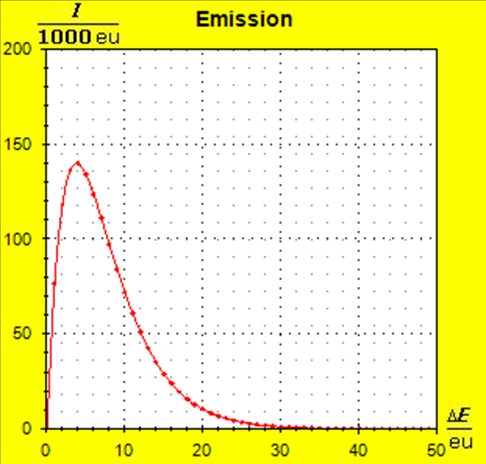
 Now, the image has changed significantly: due to the small amount of substance in the case of the aluminum, the entropy and thus the thermal inertia of this metal portion has decreased significantly. Step 5: |
|
Animation: Temperature Compensation Between Aluminum and Water |
|
Step 6: |
|
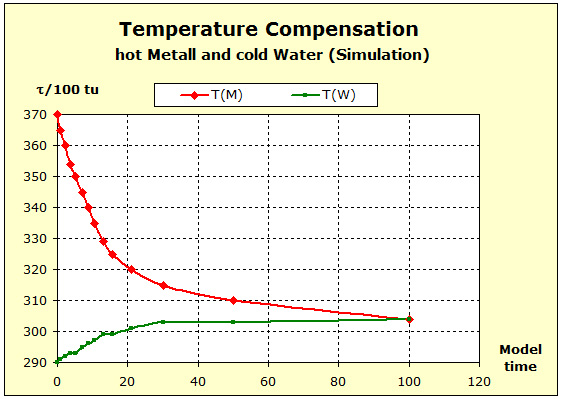 |
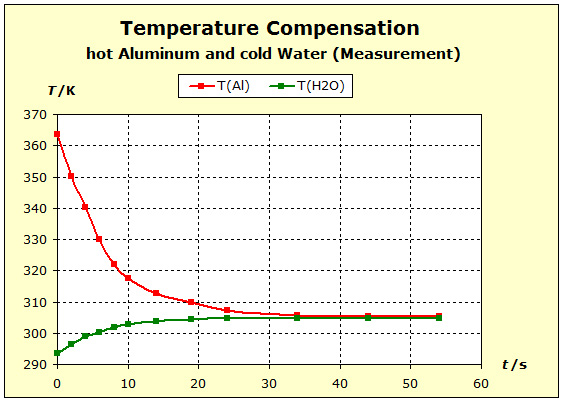 |
|
|
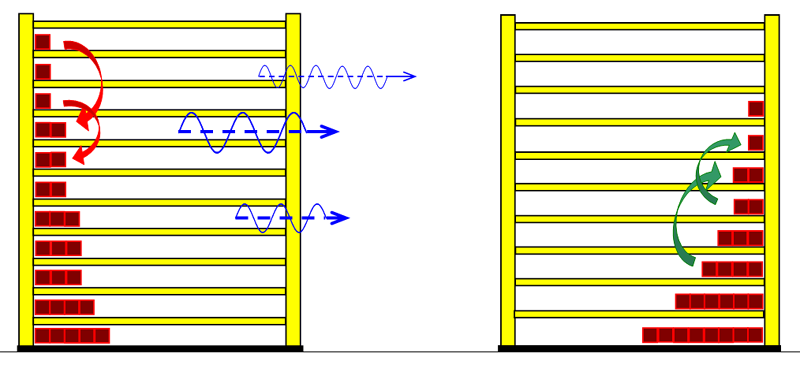
 To 3. We do not want to mix the two water portions by stiring, and therefore use a calorimeter with an intermediate wall, as is sometimes found in thermo- dynamic textbooks. The quantum theoretical background is as follows: energy is transferred from the higher energy levels of the hotter substance to the lower energy levels of the cold matter. Thus, the number of occupied energy levels, and consequently the entropies, change in both groups of matter.
To 3. We do not want to mix the two water portions by stiring, and therefore use a calorimeter with an intermediate wall, as is sometimes found in thermo- dynamic textbooks. The quantum theoretical background is as follows: energy is transferred from the higher energy levels of the hotter substance to the lower energy levels of the cold matter. Thus, the number of occupied energy levels, and consequently the entropies, change in both groups of matter.